Two bodies of masses 2 kg and 3 kg are connected by a metal wire of cross-section 0.04 mm2 and are placed on a frictionless horizontal surface. Breaking stress of metal wire is 2.5 Gpa. The maximum force F that can be applied to 3kg block so that wire does not break is Solution in Gujrati
100N
150N
200N
250N
Step by step video & image solution for Two bodies of masses 2 kg and 3 kg are connected by a metal wire of cross-section 0.04 mm^(2) and are placed on a frictionless horizontal surface. Breaking stress of metal wire is 2.5 Gpa. The maximum force F that can be applied to 3kg block so that wire does not break is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Trigonometry)22videos
RACE
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Differentiation)40videos
RACE
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Race 215videos
RACE
- BOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
Convert the angle from degree to radian :
(a) 30∘(b) 45∘(c) 60∘(d) 90∘(e) 120∘(f) 135∘(g) 210∘(h) 270∘(i) 315∘04:48View SolutionFor a straight line y=43x−4. Choose correct alternate(s)
02:31View SolutionTwo projectiles are projected with velocity vA,vB at angles θA (from horizontal) and θB (from vertical) as shown in the figure below, such that vA>vB but having same horizontal component of velocity. Which of the following is correct ?
 01:56View Solution
01:56View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.03:03View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
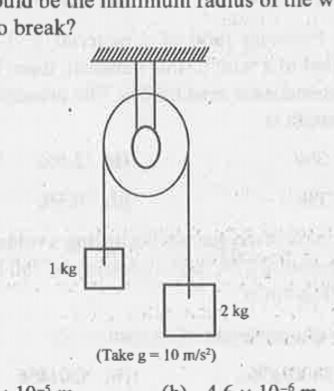
03:30View SolutionTwo blocks of masses 1 kg and 2 kg are connected by a metal wire goijng over a smooth pulley as shown in figure. The breaking stress of the metal is (40//3pi)xx10^(6)N//m^(2) . If g=10ms^(-12) , then what should be the minimum radlus of the wire used if it is not to break?
04:05View SolutionTwo bodies of masses 2kg and 3kg are connected by a metel wire of cross section 0.04 mm2. Breaking stress of metel wire is 2.5 Gpa. The maximum force F that can be applied to 3kg block so that wire does not break is :
 04:55View Solution
04:55View SolutionA force of 400 kg. weight can break a wire. The force required to break a wire of double the area of cross-section will be
03:37View SolutionTwo bodies of masses 2 kg and 3 kg are connected by a metal wire of cross-section 0.04 mm2 and are placed on a frictionless horizontal surface. Breaking stress of metal wire is 2.5 Gpa. The maximum force F that can be applied to 3kg block so that wire does not break is
02:54View SolutionThe breaking stress of a wire is 7.2xx10^(8)N//m^(2) and density is 78xx10^(2) kg//m^(3) . The wire is held vertically to the rigid support. The maximum length so that the wire does not break is
04:05View SolutionTwo block of masses 1 kg 2 are connected by a metal wire going over a smooth pulley. The breaking stress of metal is 40/(3pi) xx10^(6)Mm^(-2) . What should be the minimum radius of wire used if it should not break? (g=10ms^-2)
04:37View SolutionTwo blocks of masses 1 kg and 2 kg are connected by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109Nm−2. What should be the minimum radius of the wire used if it is not to break?
 03:18View Solution
03:18View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2xx10^(9)"N m"^(-2) . If g=10ms^(-2) , then what is the minimum radius of the wire which will not break
03:50View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
 02:42View Solution
02:42View SolutionTwo block of masses 1 kg 2 are connected by a metal wire going over a smooth pulley. The breaking stress of metal is 403π×106Mm−2 . What should be the minimum radius of wire used if it should not break?(g=10ms−2)
03:26View Solution

