A satellite of mass m revolves in a circular orbit of radius R a round a planet of mass M. Its total energy E is :-Solution in Gujrati
−GMm2R
+GMm3R
−GMmR
+GMmR
The correct Answer is:A
Step by step video & image solution for A satellite of mass m revolves in a circular orbit of radius R a round a planet of mass M. Its total energy E is :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 2
26 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 3
11 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - BOX-4
14 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
Similar Questions
Two satellites of earth S1 and S2 are moving in the same orbit. The mass of S1 is four times the mass of S2. Which one of the following statements is true?
View SolutionThe change in the value of acceleration of earth toward sun, when the moon coomes from the position of solar eclipse to the position on the other side of earth in line with sun is :
(mass of moon =7.36×1022 kg, orbital radius of moon =3.8×108 m.)
View SolutionThe mean radius of the earth's orbit round the sun is 1.5×1011 . The mean radius of the orbit of mercury round the sun is 6×1010m. The mercury will rotate around the sun in
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.
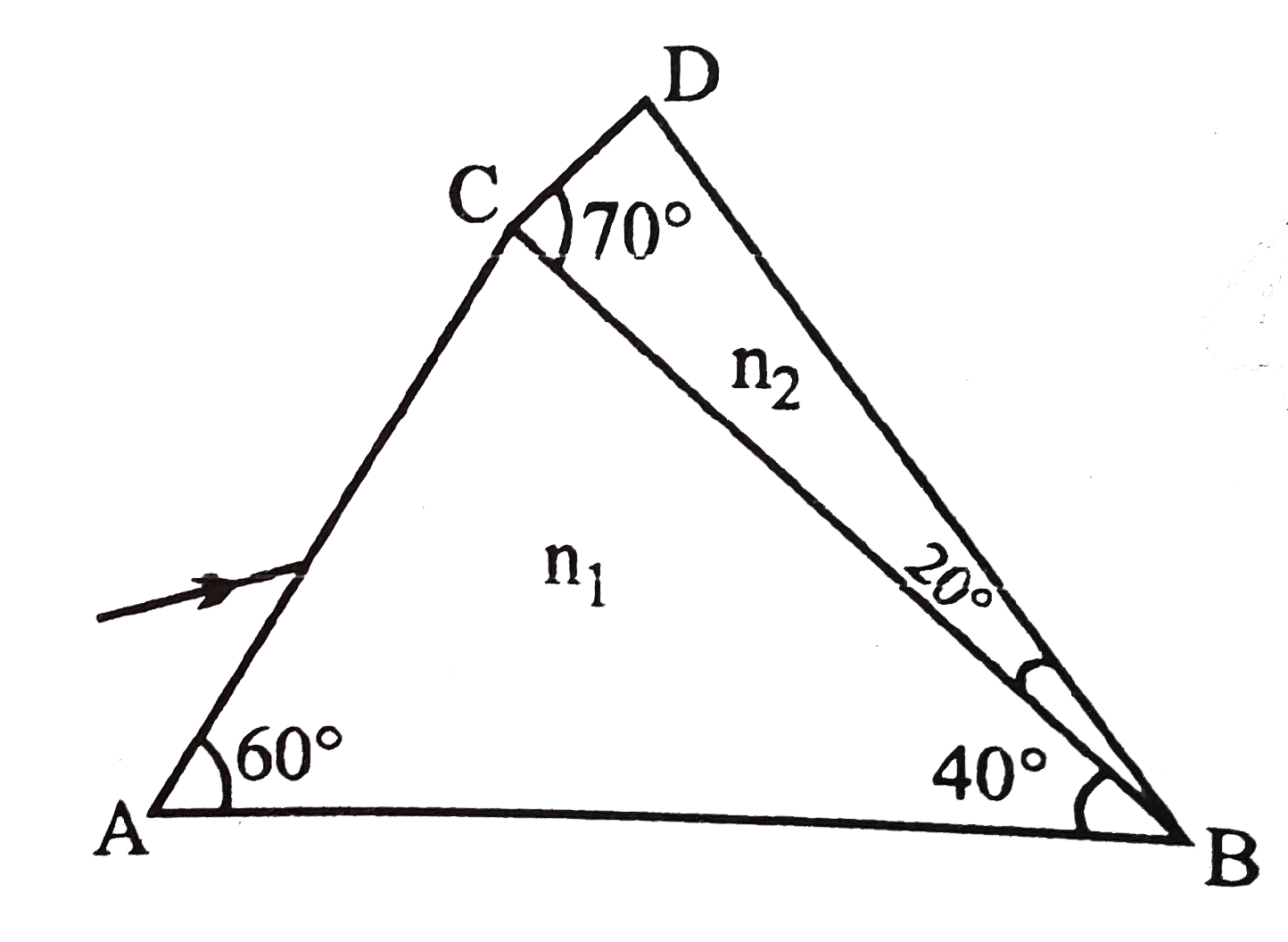
(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA satellite of mass m revolves revolves round the earth of mass M in a circular orbit of radius r with an angular velocity omega . If the angular velocity is omega//8 then the radius of the orbit will be
View SolutionA satellite of mass M revolving in a circular orbit of radius rs around the earth of mass M has a total energy E. then, its angular momentum will be
View SolutionThe satellite of mass m revolving in a circular orbit of radius r around the earth has kinetic energy E. then, its angular momentum will be
View SolutionThe total energy of an artificial satellite of mass m revolving around the earth of mass M is ……….. The radius of the orbit of the satellite =r. [Fill in the blanks]
View SolutionA satellite is orbiting round the earth in a circular orbit with speed v. If m is mass of satellite its total energy is:
View Solutionm द्रव्यमान का एक उपग्रह,M द्रव्यमान के ग्रह के चारों ओर R त्रिज्या की वृत्तीय कक्षा में घूम रहा है, तो इसकी कुल ऊर्जा E होगी :
View Solutionm द्रव्यमान का एक उपग्रह, किसी M द्रव्यमान के ग्रह की परिक्रमा R, त्रिज्या की वृत्तीय कक्षा में कर रहा है। इसकी कक्षा की त्रिज्या को R, करने के लिये (R2>R1), उपग्रह को दी जाने वाली अतिरिक्त गतिज ऊर्जा होगी :
View SolutionThe satellite of mass m revolving in a circular orbit of radius r around the earth has kinetic energy E. Then its angular momentum will be
View SolutionThe satellite of mass m revolving in a circular orbit of radius r around the earth has kinetic energy E. Then its angular momentum will be
View SolutionThe satellite of mass m revolving in a circular orbit of radius r around the earth has kinetic energy E. Then its angular momentum will be
View SolutionThe satellite of mass m revolving in a circular orbit of radius r around the earth has kinetic energy E. Then its angular momentum will be
View Solution
