
Calculate a, T1,T2,T1'&T2'.Solution in Gujrati
The correct Answer is:a=5m/sec2,T1=30N,T2=15N,T1'=30√2N,T2'=15√2N
Step by step video & image solution for Calculate a, T_(1), T_(2), T_(1)' & T_(2)'. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (FRICTION)
13 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)
33 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)
63 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
A block of mass 1 kg is plased on a surgace for which μs=0.2&μk=0.15, an external force F is applied on the block as shown in the figure, using g=10m/sec2, find:
(a) The force of friction on block
(b) Its acceleration
(i) When F=1 N
(ii) When F=2 N
(iii) When F=2.5 N

View SolutionA block of mass 2 kg is plased on a smooth horizontal surface. Two forces F1=20 N and F2=5 N start acting on the block in opposite directions as shown. If block gets displaced by 5 m in the direction of net force then work done by F2 is :-

View SolutionA man covered following displacements. Find the net displacement of the person
(i) 25m west
(ii)20m30∘ east of south
(iii)5√3m south
(iv) 10 m east
(v) 10m60∘ north of west
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View Solution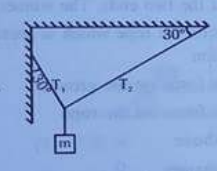
Calculate T1&T2.
View SolutionFind the matrices of transformation T1T2andT2T1 when T1 is rotation through an angle 60∘andT2 is the reflection in the Y-asix Also, verify that T1T2≠T2T1.
View SolutionIf the tangents at t1andt2 to a parabola y2=4ax are perpendicular then (t1+t2)2−(t1−t2)2=
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View Solutionयदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View SolutionFind the matrices of transformation T1T2andT2T1 when T1 is rotated through an angle 60∘andT2 is the reflection in the Y-asix Also, verify that T1T2≠T2T1.
View SolutionIf the normals at P(t_(1))andQ(t_(2)) on the parabola meet on the same parabola, then (A) t_(1)t_(2)=-1 (B) t_(2)=-t_(1)-(2)/(t_(1)) (C) t_(1)t_(2)=1 (D) t_(1)t_(2)=2
View SolutionFind the matrices of transformation T1T2andT2T1 when T1 is rotated through an angle 60∘andT2 is the reflection in the Y-asix Also, verify that T1T2≠T2T1.
View Solution
