Find the matrices of transformation T1T2andT2T1 when T1 is rotated through an angle 60∘andT2 is the reflection in the Y-asix Also, verify that T1T2≠T2T1. Solution in Punjabi
T1=[cos60∘,−sin60∘sin60∘,cos60∘]=⎡⎢⎣12−√32√3212⎤⎥⎦=12[1√3−√31]
and T2=[−1001]
∴ T1T2=12[1−√3√31]×[−1001]=12[−1+00−√3−√3+00+1]
=12[1−√3−√31]=⎡⎢⎣−12−√32−√3212⎤⎥⎦
T1T2=[−1001]×12[1−√3√31]=12[−1+0√3+00+√30+1]
=12[−1√3√31]=⎡⎢⎣−12√32√3212⎤⎥⎦
it is clear from Eqs. (i) and (ii) , then
T1T2≠T2T1
Topper's Solved these Questions
- MATRICES BOOK - ARIHANT MATHSCHAPTER - MATRICES EXERCISE - Exercise For Session 1
9 Videos
- MATRICES BOOK - ARIHANT MATHSCHAPTER - MATRICES EXERCISE - Exercise For Session 2
19 Videos
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHSCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHSCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
31 Videos
Similar Questions
If A=∣∣∣α22α∣∣∣and|A|3=125 , then the value of α is a.±1 b. ±2 c. ±3 d. ±5
View SolutionIf A=[4x+22x−3x+1] is symmetric, then x =
View SolutionIf t₁+t₅+t15+t₁₀+t₂₀+t₂₄=225 Find the sum of first 24th term of that A.P?
View SolutionThe least value of α∈R for which 4ax2+1x≥1, for all x>0, is
View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View Solution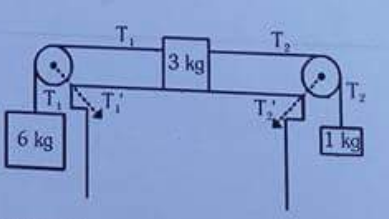
Calculate a, T1,T2,T1'&T2'.
View Solutionयदि एक वृत्त किसी समकोणीय अतिपरवलय से चार बिन्दुओं t1,t2,t3 तथा t4 में मिलता है, तो सिद्ध कीजिए कि t1,t2,t3,t4=1.
View Solutionनिम्न अनुक्रम के पहले छः पर ज्ञात कीजिए |
T1=12,T2=−1,Tn+2=Tn.Tn+1
View SolutionIf the tangents at t1andt2 to a parabola y2=4ax are perpendicular then (t1+t2)2−(t1−t2)2=
View SolutionIf the tangents at t1 and t2 on y2 = 4ax makes complimentary angles with axis then t1t2=
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View Solutionयदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View SolutionThe tangents at the points (at21,2at1),(at22,2at2) are right angles if
View Solution
Calculate a, T1,T2,T1'&T2'.
View Solution
