One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by Solution in Gujrati
CV(T1−T2)
CP(T1−T2)
CP+CV2(T1−T2)
(CP−CV)(T1−T2)
The correct Answer is:A
Step by step video & image solution for One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P_(1), V_(1), T_(1)) to the final state (P_(2), V_(2), T_(2)). The decrease in the internal energy of the gas during this process will be given by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Dscillations) (Kinematics of SHM)
20 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Oscillations) (Energy & spring pendulum)
17 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Thermal Physics) (Kinetic theory of gasess)
14 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Two particles executing SHM of same frequency meet at x=+√3A2, while moving in opposite directions. Phase difference between the particles is :-
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View SolutionFigure shows the isotherms of fixed mass of an ideal gas at three temperatures TA,TB and TC then.
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
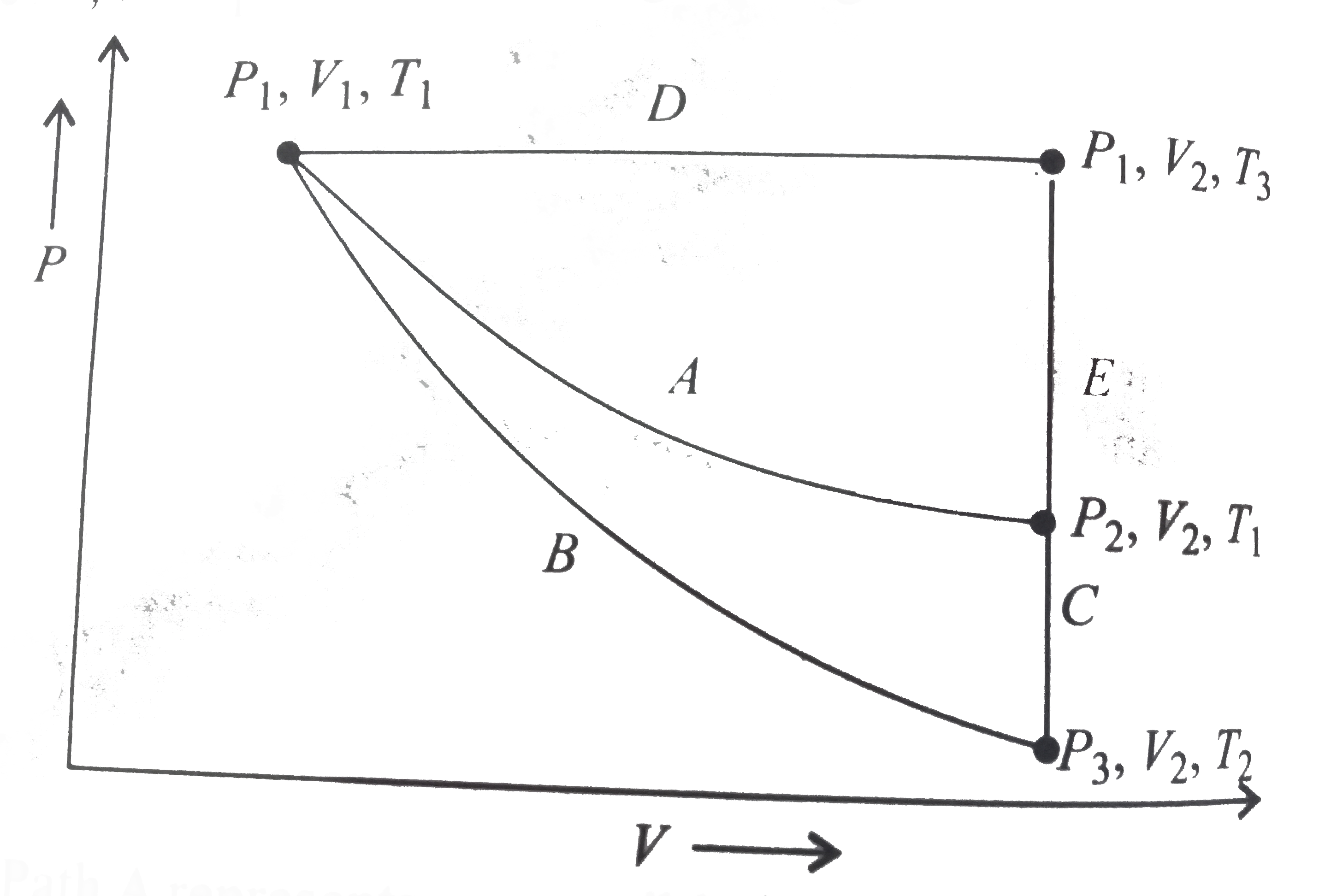
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P_(1), V_(1), T_(1) to a final state P_(2), V_(2),T_(1) is shown in the given figure. Path A represents a reversible isothermal expansion form P_(1),V_(1) to P_(2),V_(2) , Path (B+C) represents a reversible adiabatic expansion (B) from P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2) followed by reversible heating the gas at constant volume (C) from P_(3),V_(2),T_(2) to P_(2),V_(2),T_(1) . Path (D+E) represents a reversible expansion at constant pressure P_(1)(D) from P_(1),V_(1),T_(1) to P_(1),V_(2),T_(3) followed by a reversible cooling at constant volume V_(2)(E) from P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1) . What is q_(rev) , for path (B +C) ?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path A?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
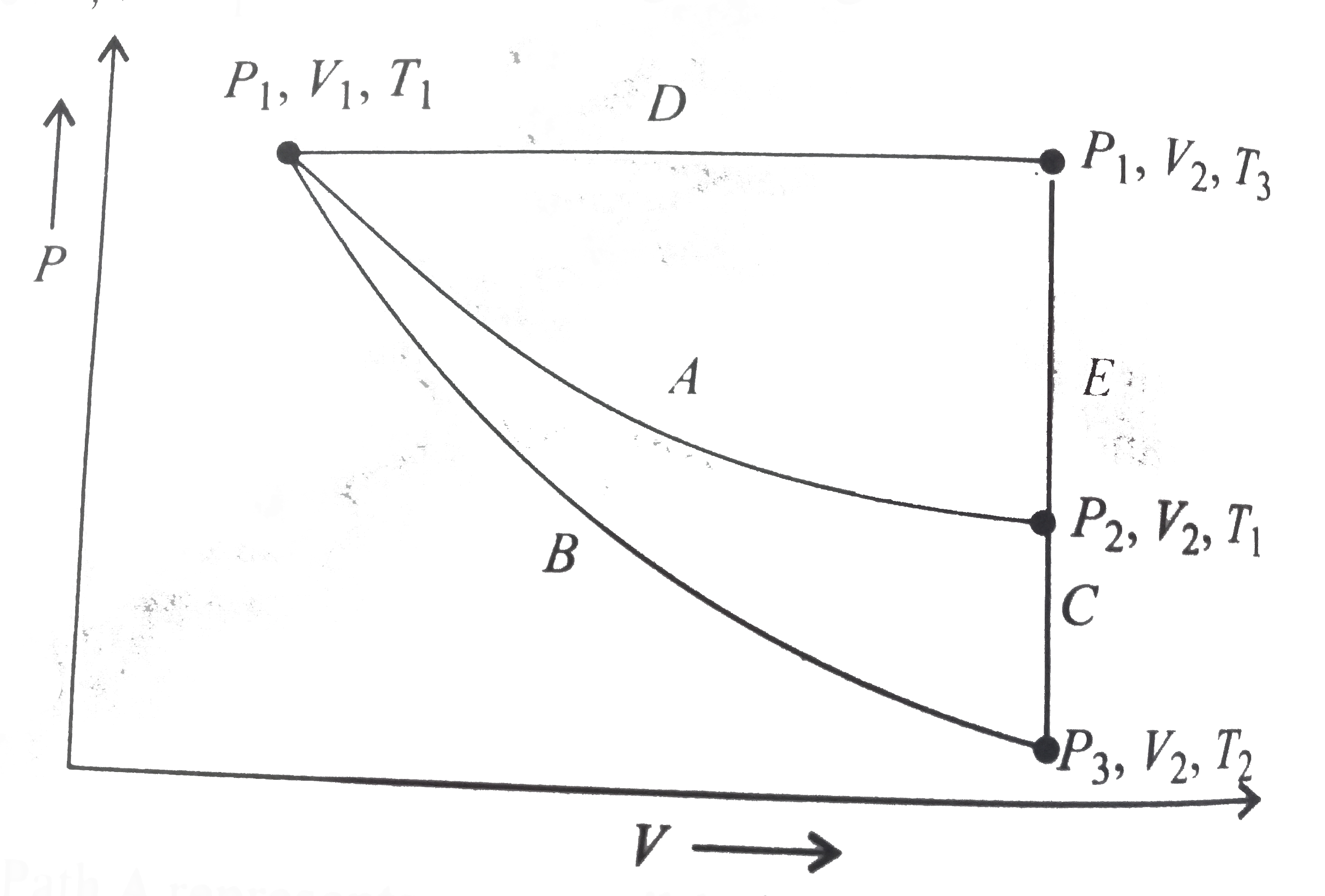
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?
View SolutionIf n moles of an ideal gas are expanded is isothermally and reversibly from an initial state in which it has pressure p1 and volume V1 to the final state of volume V2 and pressure P2, then
View SolutionOne mole of helium is adiabatically expanded from its initial state (Pi,Vi,Ti) to its final state (Pf,Vf,Tf). The decrease in the internal energy associated with this expansion is equal to
View SolutionIn an adiabatic process, the state of a gas is changed from P_(1),V_(1),T_(1), "to" P_(2),V_(2),T_(2). Which of the following relation is correct
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
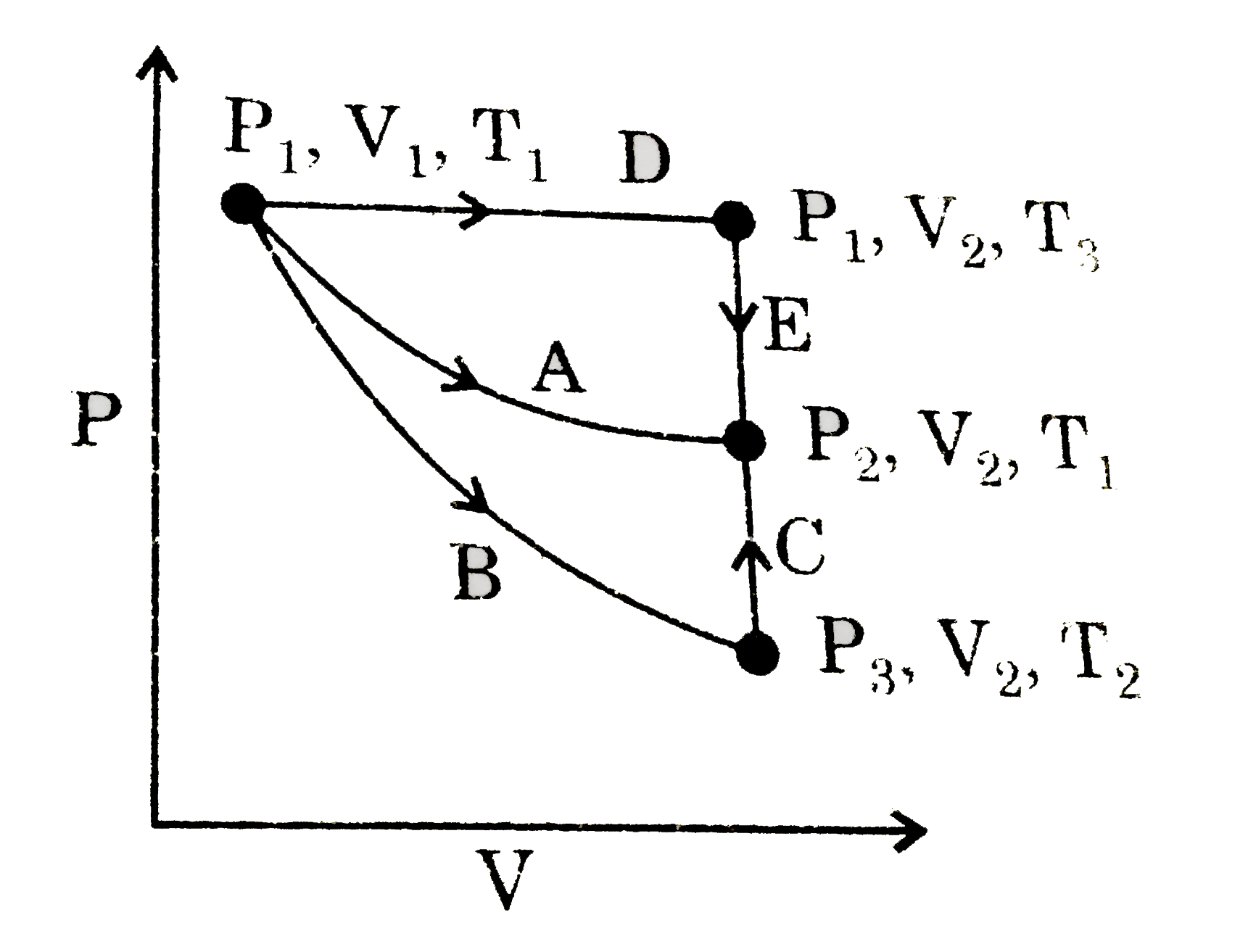
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for (D+E)?
View SolutionIn an adiabatic process the state of a gas is changed from P_(1) , V_(1) ,T_(1) , to P_(2) ,V_(2) ,T_(2). Which of the following relation is correct ?
View SolutionThe initial pressure, temperature & volume of 1 mol of a gas are P1,T1andV1 respectively. The state of the gas is changed by the following two ways. Will the internal energy change be the same in both cases?
(1) P1V1T2Reversible−−−−−→ProcessP2V2T2
(2) P1V1T1Irreversible−−−−−−→processP2V2T2.
View SolutionThe initial state of 1 mol of an ideal gas is (P_(1),V_(1),T_(1)) . The gas is expanded by a reversible isothermal process and also by a reversible adiabatic process separately. If final volume of the gas is same in both the processes, and changes in internal energy in the isothermal and adiabatic processes are DeltaU_(1) and DeltaU_(2) respectively, then-
View Solution
