For a certain process pressure of diatomic gas varies according to the relation P=aV2, where a is constant. What is the molar heat capacity of the gas for this process?Solution in Gujrati
17R6
6R17
13R6
16R7
The correct Answer is:A
Step by step video & image solution for For a certain process pressure of diatomic gas varies according to the relation P=aV^(2), where a is constant. What is the molar heat capacity of the gas for this process? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Dscillations) (Kinematics of SHM)
20 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Oscillations) (Energy & spring pendulum)
17 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Thermal Physics) (Kinetic theory of gasess)
14 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
Two particles executing SHM of same frequency meet at x=+√3A2, while moving in opposite directions. Phase difference between the particles is :-
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View SolutionFigure shows the isotherms of fixed mass of an ideal gas at three temperatures TA,TB and TC then.
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionOne mole of a diatomic gas is heated under a "kibolinsky process" in which gas pressure is temperature controlled according to law P=(4)/(5)CT^(3//2) . Where C is kibolinsky constant. In this process, gas is heated by 300K temperature. Answer the following questions. Under above a process the molar specific heat of gas is:
View SolutionAn ideal diatomic gas undergoes a process in which the pressure is proportional to the volume. Calculate the molar specific heat capacity of the gas for the process.
View SolutionThe molar heat capacity of a perfect gas at constant volume is Cv. The gas is subjected to a process T=T0eAV, Where T0 and A are constant. Calculate the molar heat capacity of the gas a function of its volume
View SolutionFor a certain process pressure of diatomic gas varies according to the relation P=aV^(2n) , where a is constant. What is the molar heat capacity of the gas for this process?
View SolutionP - V diagram of a diatomic gas is a straight line parallel to P-axis. The molar heat capacity of the gas in the process will be
View SolutionThe pressure P of an ideal diatomic gas varies with its absolute temperature T as shown in figure. The molar heat capacity of gas during this process is [R is gas constant]
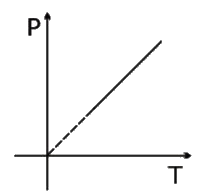
View SolutionA monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
View SolutionFor a certain process, pressure of diatomic gas varies according to the relation P=aV2, where a is constant. What is the molar heat capacity of the gas for this process ?
View SolutionP-V diagram of a diatomic gas is a straight line passing through origin. What is the molar heat capacity of the gas in the process
View SolutionAn ideal diatomic gas is taken through a process in which the pressure and the volume vary as P = aV^b . If the specific heat capacity in the process is zero, then (-5b) is equal to ______
View SolutionP-V diagram of a diatomic gas is a straight line passing through origin. What is the molar heat capacity of the gas in the process
View Solution