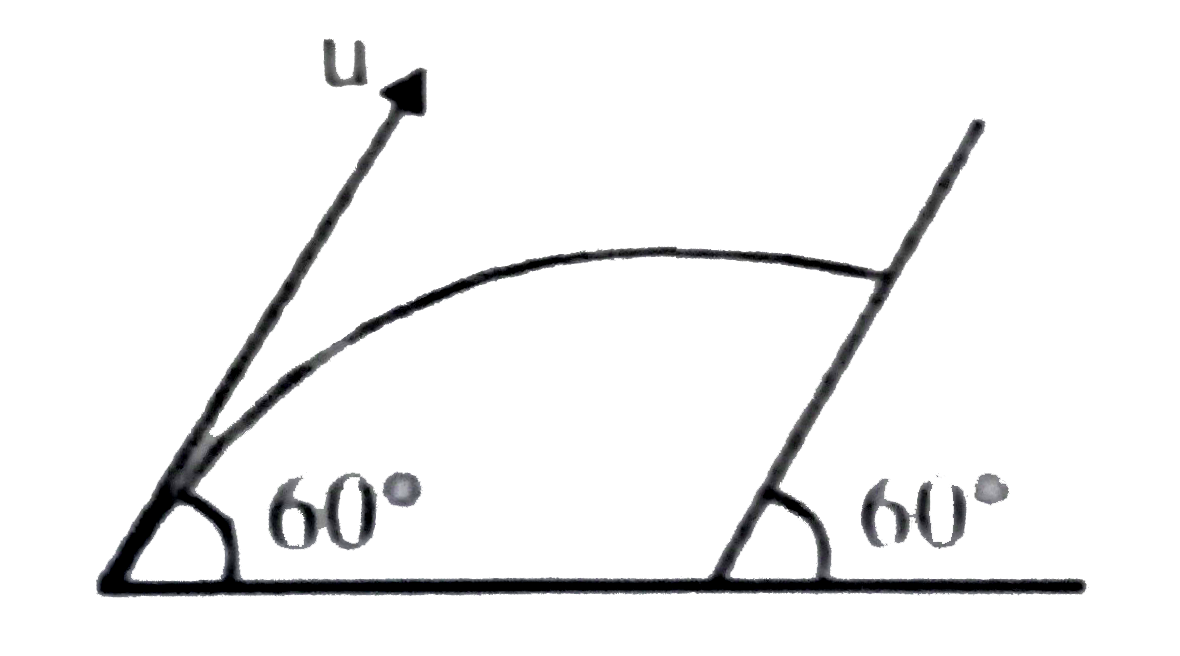
A particle is projected at an angle 60∘ from Horizon from ground with speed u. after some time it collides with a wall inclined at an angle 30∘ from horizon. At the time of collision velocity of particle is perpendicular to the wall. Find speed of the particle at the time of collision :-
 Solution in Gujrati
Solution in Gujrati
u
u√3
2u√3
2u
The correct Answer is:B
Step by step video & image solution for A particle is projected at an angle 60^@ from Horizon from ground with speed u. after some time it collides with a wall inclined at an angle 30^@ from horizon. At the time of collision velocity of particle is perpendicular to the wall. Find speed of the particle at the time of collision :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle is projected vertically upwards with a velocity v. It returns to the ground in time T. Which of the following graphs correctly represents the motion.
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
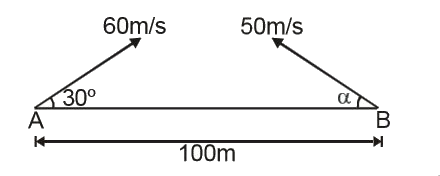
View SolutionA particle A is projected with an initial velocity of 60m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g=10m/s2)

View SolutionA particle is projected from surface of the inclined plane with speed u and at an angle theta with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).
View SolutionA particle is thrown with speed u at an angle α with horizontal from the ground. After how much time, the velocity of particle will make an angle β with horizontal.
View SolutionA particle is pojected from the ground at an angle of θ with the horizontal with an initial speed of u. Time after which velocity vector of the projectile is perpendicular to the initial velocity is
View SolutionA particle is projected from ground with speed u and at an angle θ with horizontal. If at maximum height from ground, the speed of particle is 1/2 times of its initial velocity of projection, then find its maximum height attained.
View SolutionA particle A is projected with an initial velocity of 60m/s at angle 30∘ to the horizontal . At the same time a second particle B is projected in opposite directions with initial speed of 50m/s from a point at a distance of 100m from A.
if the particle collides in air,

Answer the following questions:
Time of collisions will be:
View SolutionA particle is projected from a point A with velocity u√2 at an angle of 45∘ with horizontal as shown in the figure. It strikes the plane BC at right angles. The velocity of the particle at the time of collision is

View SolutionA particle is projected from the ground with speed u at angle 60∘ from horizontal. It collides with a second particle of same mass moving with horizontal speed u in same direction at highest point of its trajectory. If collision is perfectly inelastic then find horizontal distance travelled by them after collision when they reached at ground
View SolutionA particle A is projected with an initial velocity of 60 m/s. at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection ∝ of particle B,
View SolutionA particle is projected from the surface of the earth with a speed of 20 m* s^(-1) at an angle 30^@ with the horizontal . The time of flight of that particle is
View SolutionA particle of unit mass is projected with velocity u at an inclination alpha above the horizon in a medium whose resistance is k times the velocity. Its direction will again make an angle alpha with the horizon after a time
View SolutionA particle is projected from the ground with an initial speed of 5ms−1 at an angle of projection 60° with horizontal. The average velocity of the particle between its time of projection and the time it reaches highest point of trajectory
View SolutionA particle is projected from the ground with speed u at angle 60∘ from horizontal. It collides with a second particle of same mass moving with horizontal speed u in same direction at highest point of its trajectory. If collision is perfectly inelastic then find horizontal distance travelled by them after collision when they reached at ground
View SolutionA particle A is projected with an initial velocity of 60 m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with intial speed of 50 m/s from a point at a distance of 100 m from A. if the particles collide in air, find a the angle of projection α of particle B (b) time when the collisions takes place and c the distance of P from A. where collision occurs (g=10m/s2)

View Solution
