Two masses are attached to a rod end to end . If torque is applied they rotate with angular acceleration α. If their distances are doubled and same torque is applied, then they move with angular acceleration.
4α
α
3α
α/4
The correct Answer is:D
To solve the problem step by step, we will analyze the situation using the concepts of torque and moment of inertia.
Step 1: Define the initial conditions
Let the two masses be m1 and m2 attached to a rod at distances r from the axis of rotation. The torque τ applied to the system results in an angular acceleration α.
Step 2: Calculate the moment of inertia for the initial configuration
The moment of inertia I1 for the two masses is given by the formula:
I1=m1r2+m2r2=(m1+m2)r2
Step 3: Relate torque and angular acceleration for the initial configuration
Using the relationship between torque, moment of inertia, and angular acceleration:
τ=I1α
Substituting I1:
τ=(m1+m2)r2α
Step 4: Define the new conditions after doubling the distances
Now, the distances of the masses from the axis of rotation are doubled, so they are at 2r. The new moment of inertia I2 is calculated as:
I2=m1(2r)2+m2(2r)2=m1⋅4r2+m2⋅4r2=(m1+m2)⋅4r2
Step 5: Relate torque and angular acceleration for the new configuration
The same torque τ is applied, so we have:
τ=I2α′
Substituting I2:
τ=(m1+m2)⋅4r2α′
Step 6: Set the two torque equations equal to each other
Since the torque is the same in both cases:
(m1+m2)r2α=(m1+m2)⋅4r2α′
Step 7: Simplify the equation
We can cancel (m1+m2) and r2 from both sides (assuming they are not zero):
α=4α′
Step 8: Solve for the new angular acceleration
Rearranging gives:
α′=α4
Conclusion
Thus, when the distances are doubled and the same torque is applied, the new angular acceleration α′ is:
α′=α4
Let the two masses be m1 and m2 attached to a rod at distances r from the axis of rotation. The torque τ applied to the system results in an angular acceleration α.
The moment of inertia I1 for the two masses is given by the formula:
I1=m1r2+m2r2=(m1+m2)r2
Using the relationship between torque, moment of inertia, and angular acceleration:
τ=I1α
Substituting I1:
τ=(m1+m2)r2α
Now, the distances of the masses from the axis of rotation are doubled, so they are at 2r. The new moment of inertia I2 is calculated as:
I2=m1(2r)2+m2(2r)2=m1⋅4r2+m2⋅4r2=(m1+m2)⋅4r2
The same torque τ is applied, so we have:
τ=I2α′
Substituting I2:
τ=(m1+m2)⋅4r2α′
Since the torque is the same in both cases:
(m1+m2)r2α=(m1+m2)⋅4r2α′
We can cancel (m1+m2) and r2 from both sides (assuming they are not zero):
α=4α′
Rearranging gives:
α′=α4
Thus, when the distances are doubled and the same torque is applied, the new angular acceleration α′ is:
α′=α4
Similar Questions
In first figure a meter stick, half of which is wood and the other half steel is pivoted at the wooden end at A and a force is applied at the steel and at O. On second figure the stick is pivoted at the steel end at O and the same force is applied at the wooden end at A. The angular acceleration.
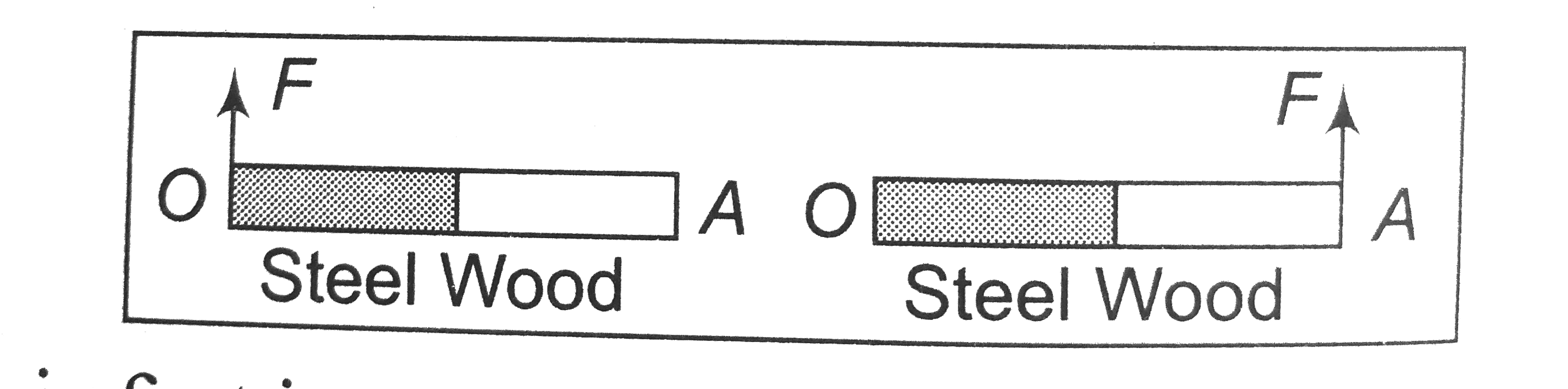 .
.
View SolutionA particle is at a distance r from the axis of rotation. A given torque τ produces some angular acceleration in it. If the mass of the particle is doubled and its distance from the axis is halved, the value of torque to produce the same angular acceleration is -
View SolutionA particle of mass M and radius of gyration K is rotating with angular acceleration α. The torque acting on the particle is
View SolutionCompute the angular acceleration of a wheel having moment of inertia 20kgm2, when a torque of 10Nm is applied on the wheel.
View SolutionCompute the angular acceleration of a wheel having moment of inertia 20kgm2, when a torque of 10Nm is applied on the wheel.
View SolutionDerive the equations of rotational motion for a body moving with uniform angular acceleration,
View SolutionTwo identical masses are connected to a horizontal thin massless rod as shown in the figure. When their distance from the pivot is x, a torque produces an angular acceleration α1. If the masses are now repositioned so that they are at distance 2x each from the pivot, the same torque will produce an angular acceleration α2 such that ,

View Solutionthe angular acceleration of flywheel having moment of inertia 50 kg m2 when a torque of 5 N−m is applied on the flywheel is
View SolutionThe angular velocity and angular acceleration of the pivoted rod are given as ω and α respectively. Fid the x and y components of acceleration of B.
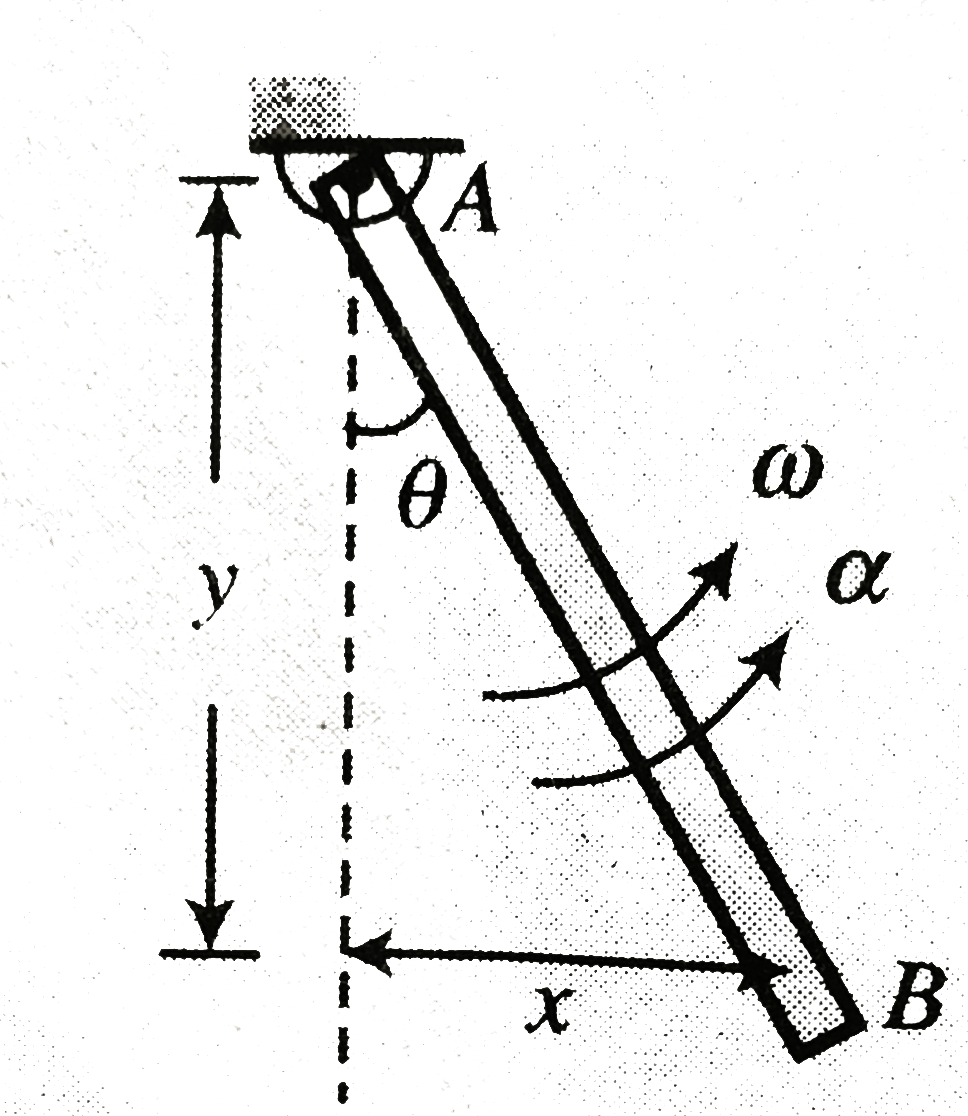
View SolutionShow that the torque acting on a body is equal to the product of moment of inertia and the angular acceleration of the body.
View Solution
