Compute the angular acceleration of a wheel having moment of inertia 20kgm2, when a torque of 10Nm is applied on the wheel.
To compute the angular acceleration of the wheel, we can use the relationship between torque, moment of inertia, and angular acceleration. The formula we will use is:
τ=I⋅α
Where:
- τ is the torque applied,
- I is the moment of inertia,
- α is the angular acceleration.
1. Identify the given values:
- Moment of inertia I=20kg m2
- Torque τ=10Nm
2. Use the formula for angular acceleration:
Rearranging the formula τ=I⋅α to solve for α:
α=τI
3. Substitute the known values into the equation:
α=10Nm20kg m2
4. Perform the calculation:
α=1020=0.5radians per second2
5. Conclusion:
The angular acceleration of the wheel is 0.5radians per second2.
- τ is the torque applied,
- I is the moment of inertia,
- α is the angular acceleration.
- Moment of inertia I=20kg m2
- Torque τ=10Nm
Rearranging the formula τ=I⋅α to solve for α:
α=τI
α=10Nm20kg m2
α=1020=0.5radians per second2
The angular acceleration of the wheel is 0.5radians per second2.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
the angular acceleration of flywheel having moment of inertia 50 kg m2 when a torque of 5 N−m is applied on the flywheel is
View SolutionCompute the torque acting on a wheel of moment of inertia 10kgm2, moving with angular acceleration 5rads−2.
View SolutionCompute the torque acting on a wheel of moment of inertia 10kgm2, moving with angular acceleration 5rads−2.
View SolutionCalculate the instantenous power of a wheel rotating with an angular velocity of 20rad/s, when a torque of 10Nm is applied to it.
View SolutionCalculate the instantenous power of a wheel rotating with an angular velocity of 20rad/s, when a torque of 10Nm is applied to it.
View SolutionThe torque required to stop a wheel having moment of inertia 5×10−3kgm2 from a speed of 10 radian s−1 in 20s is
View SolutionThe drwing shows a bicycle wheel of radius r, resting against a small step whose height is h=r/5. A clockwise torque increases, there comes a time when the wheel just begins to rise up and loses contact with the ground. Let this torque be T. What is the magniitude of the horizontal component of the acceleration of the centre of the wheel when a torque of 2T is applied? Assume that the wheel doesn't slip at the edge of the step when this torque is applied (ignore the mass of the spokes).

View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
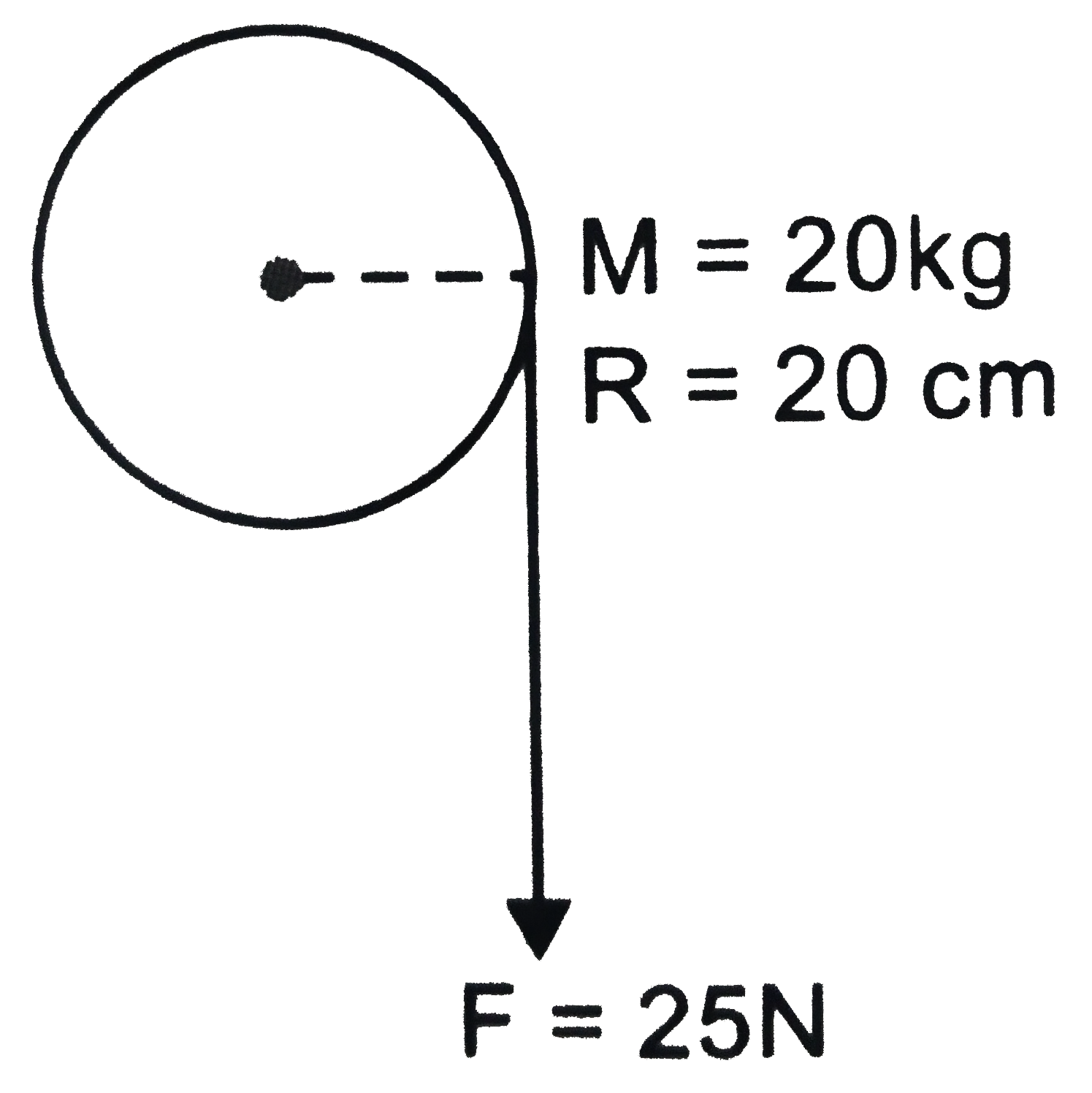
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionTwo masses are attached to a rod end to end . If torque is applied they rotate with angular acceleration α. If their distances are doubled and same torque is applied, then they move with angular acceleration.
View SolutionA wheel of radius 10 cm can rotate freely about its centre as shown in figure. A string is wrapped over its rim and is pulled by a force of 5.0 N. It is found that the torque produces an angular acceleration 2.0 rads−2 in the wheel. Calculate the moment of inertia of the wheel.

View Solution
