An astronaut is looking down on earth's surface from a space shuttle at an altitude of 400km. Assuming that the astronaut's pupil diameter is 5mm and the wavelength of visible light is 500nm. The astronaut will be able to resolve linear object of the size of about .
0.5m
5m
50m
500m
The correct Answer is:C
To solve the problem of determining the smallest linear object that an astronaut can resolve while looking down at the Earth's surface from a space shuttle at an altitude of 400 km, we will use the formula for resolving power.
1. Identify the Given Values:
- Altitude of the astronaut (D) = 400 km = 400×103 m
- Diameter of the astronaut's pupil (d) = 5 mm = 5×10−3 m
- Wavelength of visible light (λ) = 500 nm = 500×10−9 m
2. Use the Resolving Power Formula:
The formula for resolving power (R_p) is given by:
Rp=1.22⋅λ⋅Dd
3. Substitute the Values into the Formula:
Plugging in the values we have:
Rp=1.22⋅(500×10−9)⋅(400×103)5×10−3
4. Calculate the Numerator:
First, calculate the numerator:
1.22⋅500×10−9⋅400×103=1.22⋅500⋅400⋅10−6
=1.22⋅200000=244000 (approximately)
5. Calculate the Denominator:
The denominator is:
5×10−3=0.005
6. Final Calculation:
Now, divide the numerator by the denominator:
Rp=2440000.005=48800000 (approximately)
7. Convert to Meters:
Since the resolving power is in meters, we can express it as:
Rp≈48.8 m
8. Conclusion:
The astronaut will be able to resolve linear objects of size approximately 50 meters.
Final Answer:
The astronaut will be able to resolve linear objects of size about 50 meters.
- Altitude of the astronaut (D) = 400 km = 400×103 m
- Diameter of the astronaut's pupil (d) = 5 mm = 5×10−3 m
- Wavelength of visible light (λ) = 500 nm = 500×10−9 m
The formula for resolving power (R_p) is given by:
Rp=1.22⋅λ⋅Dd
Plugging in the values we have:
Rp=1.22⋅(500×10−9)⋅(400×103)5×10−3
First, calculate the numerator:
1.22⋅500×10−9⋅400×103=1.22⋅500⋅400⋅10−6
=1.22⋅200000=244000 (approximately)
The denominator is:
5×10−3=0.005
Now, divide the numerator by the denominator:
Rp=2440000.005=48800000 (approximately)
Since the resolving power is in meters, we can express it as:
Rp≈48.8 m
The astronaut will be able to resolve linear objects of size approximately 50 meters.
The astronaut will be able to resolve linear objects of size about 50 meters.
Similar Questions
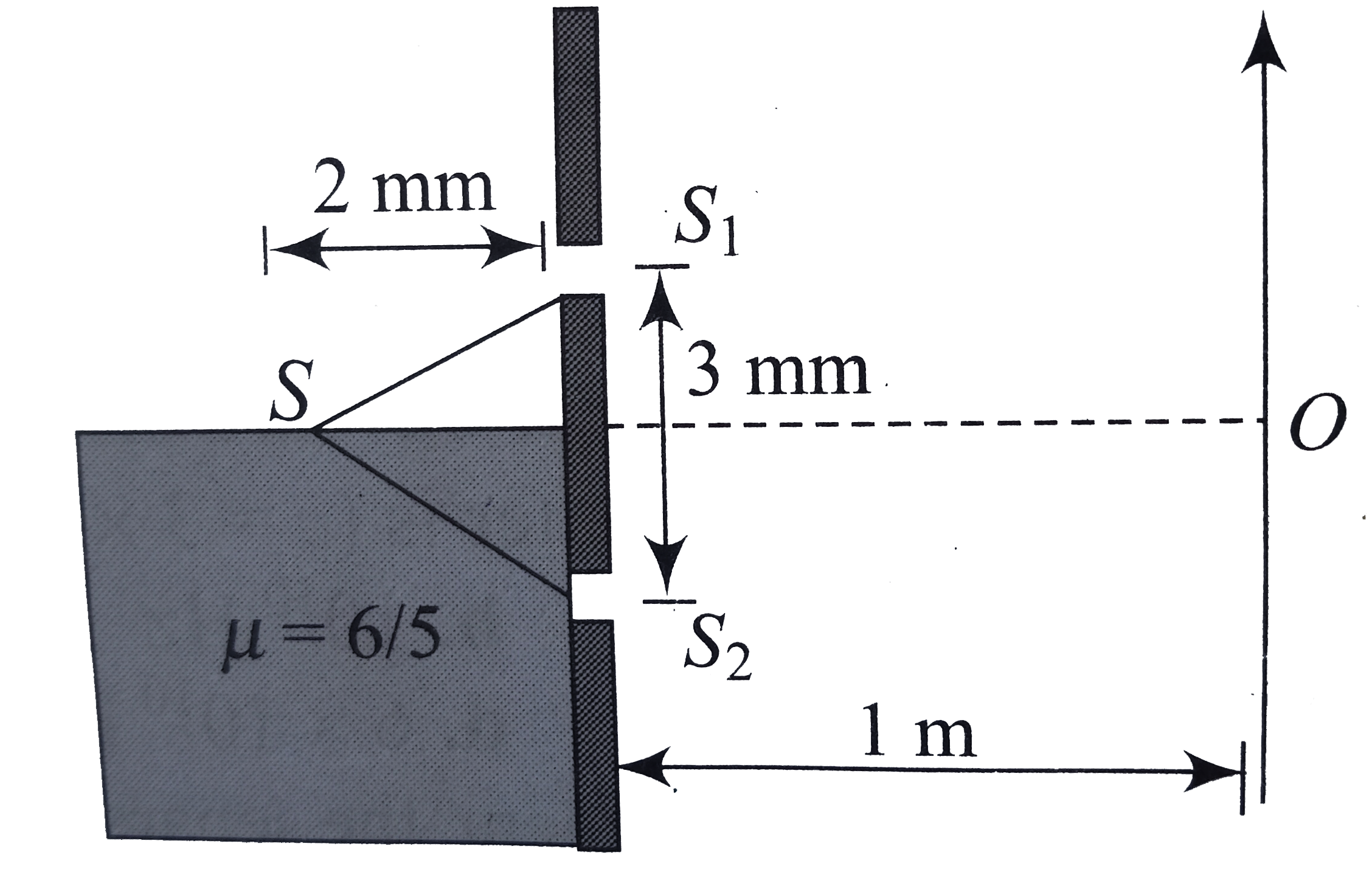
In Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distacne from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.
View SolutionA cord of length 64m is used to connected a 100kg astronaut to spaceship whose mass is much larger than that of the astronuat. Estimate the value of the tension in the cord. Assume that the spaceship is orbiting near earth surface. Assume that the spaceship and the astronaut fall on a straight line from the earth centre. the radius of the earth is 6400km.
View SolutionIf aperture diameter of telescope is 10m and distance Moon and Earth is 4×105Km. With wavelength of lightis 5500Å. The minimum separation between objects on surface of Moon, so that they are just resolved is close to :
View SolutionIf aperture diameter of telescope is 10m and distance Moon and Earth is 4×105Km. With wavelength of lightis 5500Å. The minimum separation between objects on surface of Moon, so that they are just resolved is close to :
View SolutionTwo stars are 10 light years away from the earth. They are seen through a telescope of objective diameter 30 cm. The wavelength of light is 600nm. To see the stars just resolved by the telescope, the minimum distance between them should be (1 light year =9.46×1015m) of the order of :
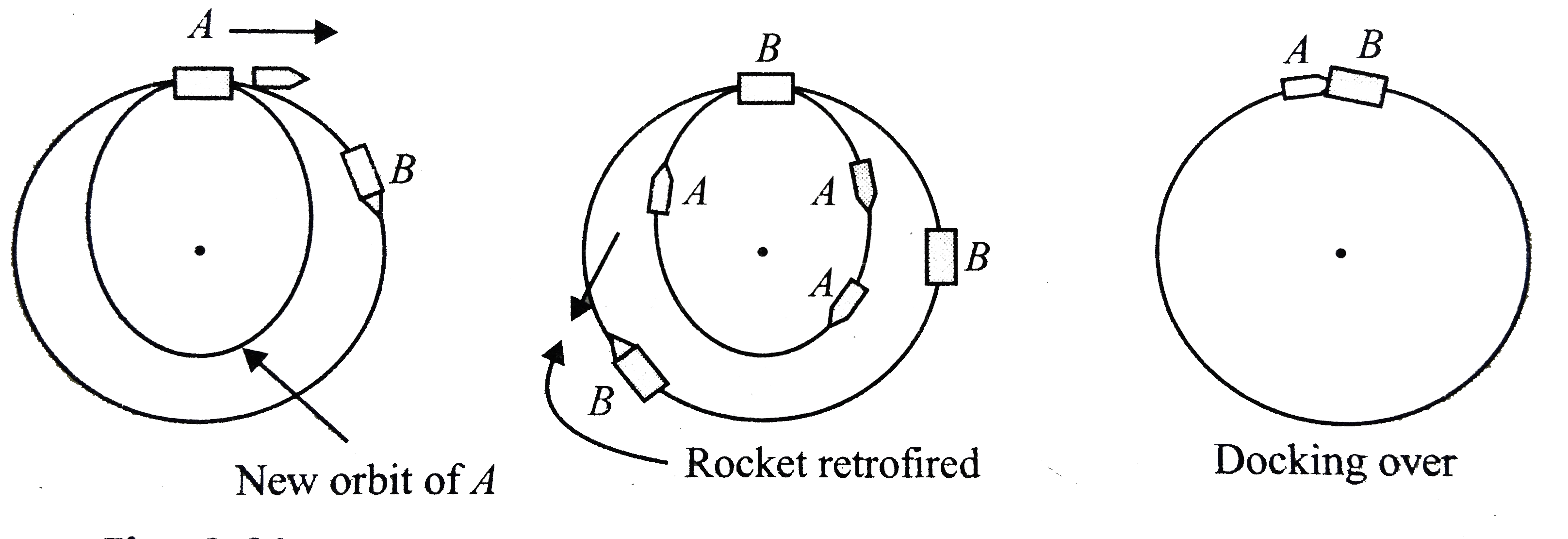
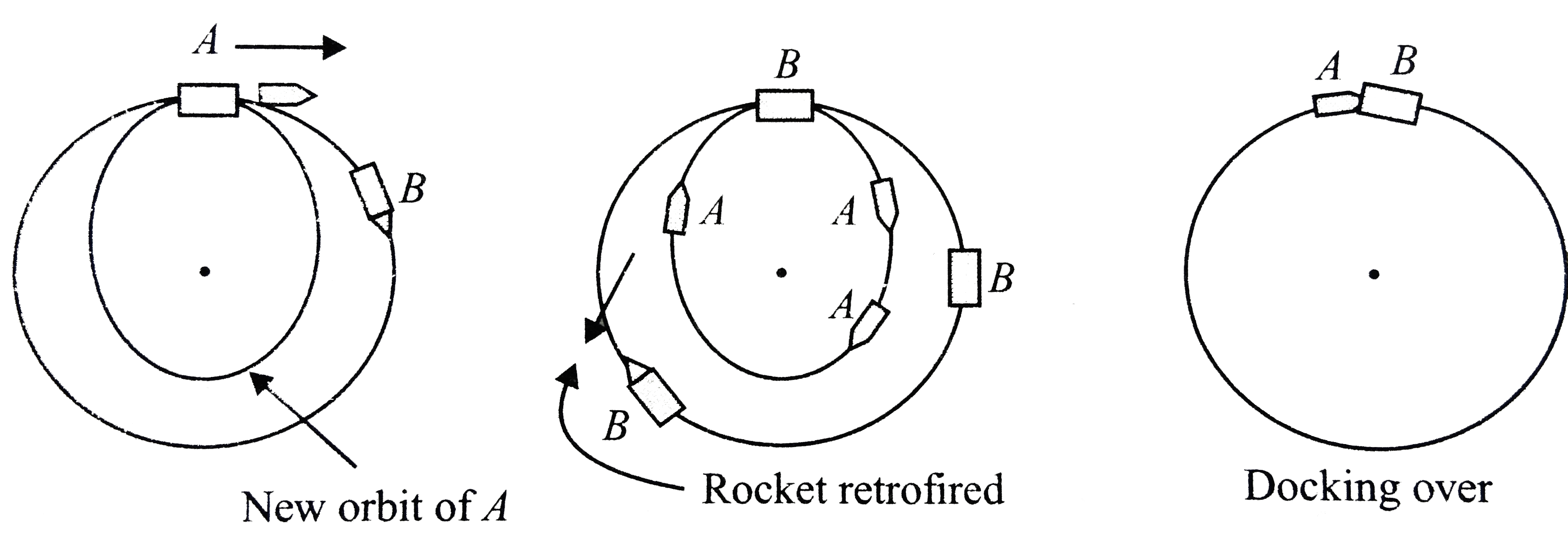
View SolutionAn unmanned satellite A and a spacecraft B are orbiting around the earth in the same circular orbit as shown.
 The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
Take mass of the earth =5.98×1024kg
Radius of the earth =6400km
Orbital radius =9600km
Mass of satellite A=320kg
Mass of spacecraft =3200kg
Assume that initially spacecraft B leads satellite A by 100s, i.e., A arrives at any particle position after 100s of B’s arrival. Based on the above information answer the following questions
The initial total energy and time period of satellite are, respectively,
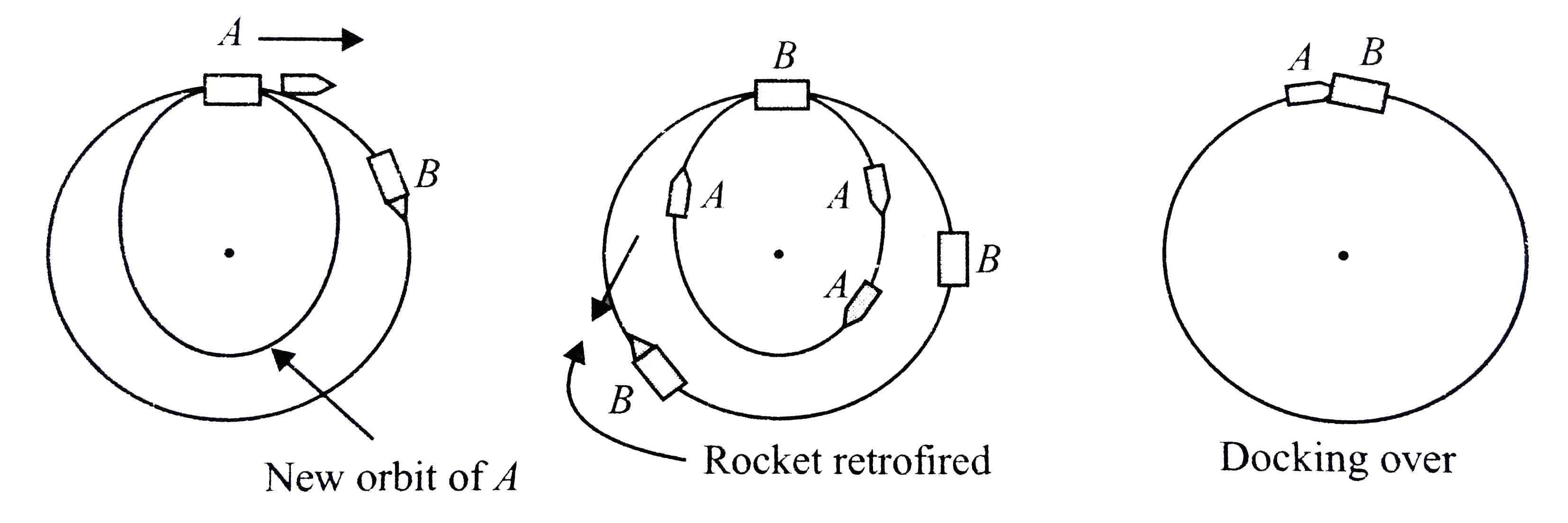
View SolutionAn unmanned satellite A and a spacecraft B are orbiting around the earth in the same circular orbit as shown.
 The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
Take mass of the earth =5.98×1024kg
Radius of the earth =6400km
Orbital radius =9600km
Mass of satellite A=320kg
Mass of spacecraft =3200kg
Assume that initially spacecraft B leads satellite A by 100s, i.e., A arrives at any particle position after 100s of B’s arrival. Based on the above information answer the following questions. After once returning to the original point, i.e., the place from where the rockets have been fired, in which direction and with what extent the rockets have to be fired from the satellite to again come back in the original orbit?
View SolutionAn unmanned satellite A and a spacecraft B are orbiting around the earth in the same circular orbit as shown.
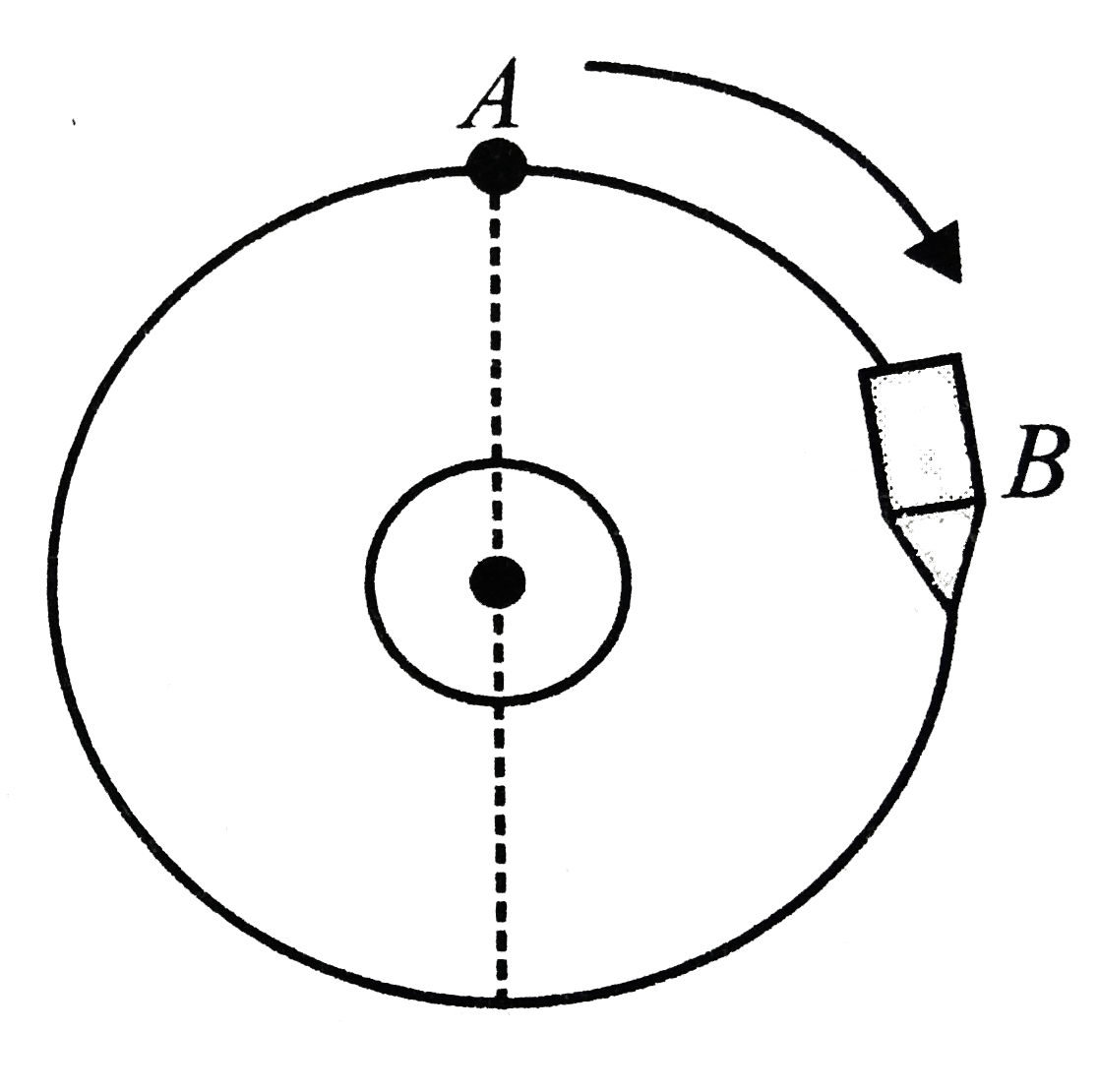 The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
Take mass of the earth =5.98×1024kg
Radius of the earth =6400km
Orbital radius =9600km
Mass of satellite A=320kg
Mass of spacecraft =3200kg
Assume that initially spacecraft B leads satellite A by 100s, i.e., A arrives at any particle position after 100s of B’s arrival. Based on the above information answer the following questions.
To dock A and B in the above-described situation, one can use the rocket system of either one, i.e., either of A or of B. To accomplish docking in the minimum possible time which is the best way?
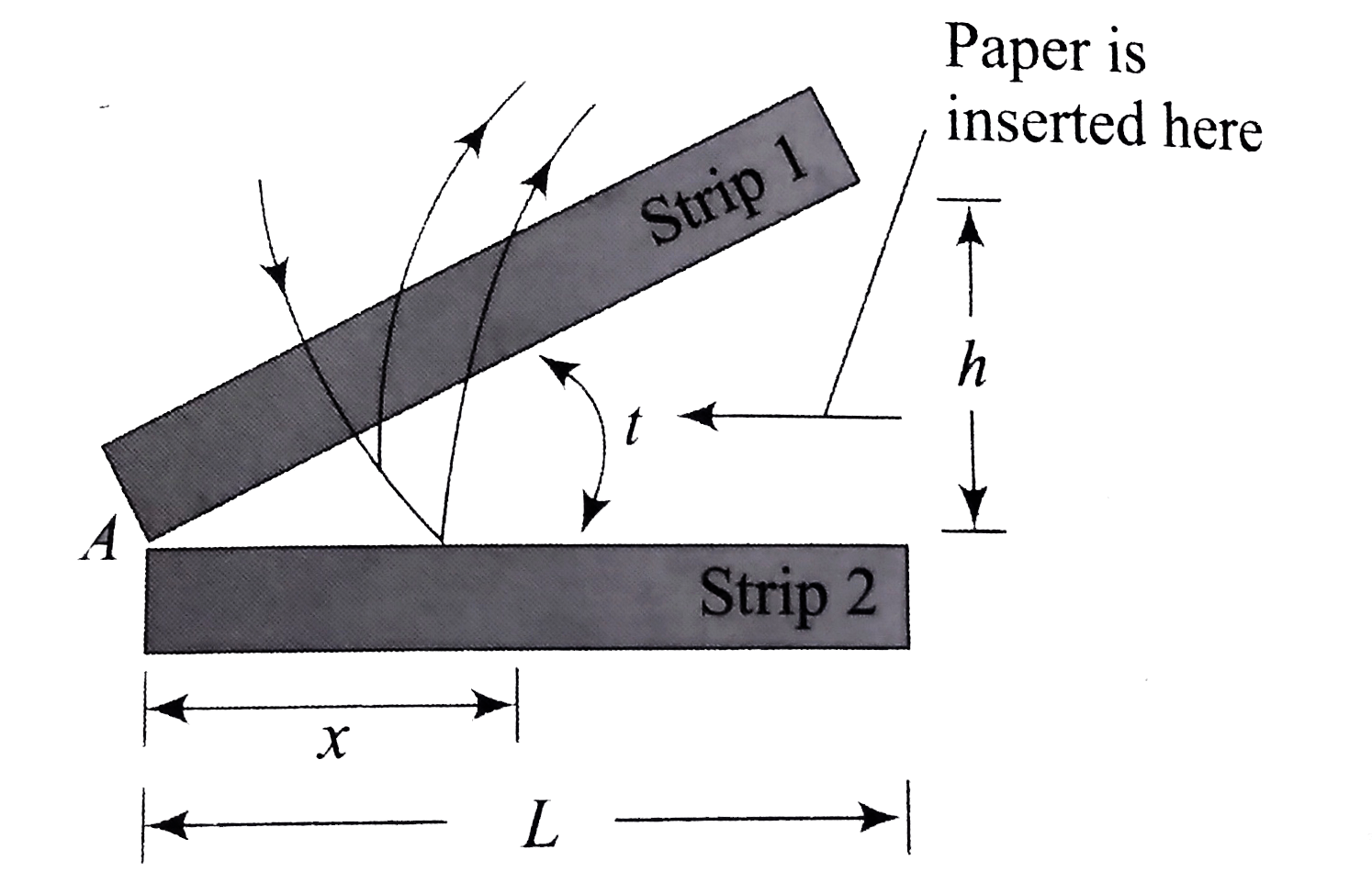
View SolutionThis interference film is used to measure the thickness of slides, paper, etc. The arrangement is as shown in fig. For the sake of clarity, the two strips are shown thick. Consider the wedge formed in between strips 1 and 2. If the interference pattern because of the two waves reflected from wedge surface is observed, then from the observed data we can compute thickness of paper, refractive index of the medium filled in wedge, number of bonds formed, etc.
Considre the strips to be thick as compared to wavelength of ligth and light is incident normally.
Neglect the effect due to reflection from top surface of strip 1 and bottom surface of strip 2. Take L=5cm and λair=400nm ,h=20mm.
In question 53, if air wedge has been filled with a medium having refractive index 1.3 then find the number of bright bands.
View SolutionAn astronaut whose height is 1.50 m floats ''feet down'' in an orbiting space shuttle at a distance r=3√6.67×106m away from the centre of Earth. The gravitational acceleration at her feet and at her head is found to be N×10−6ms−2. What is the value of N ?
[ME=6×1024 kg and G=6.67×10−11N m2kg−2]
View Solution
