A converging lens forms a real image I on its optic axis. A rectangular galss slab of refractive index μ and thickness t is introduced between the lens and I. I will move
towards the lens (μ−1)x
towards the lens by (1−1μ)x
anway from the lens by (μ−1)
away from the lens by (1−1μ)x
The correct Answer is:D
To solve the question regarding the movement of the image I when a rectangular glass slab of refractive index μ and thickness t is introduced between a converging lens and the image, we can follow these steps:
1. Understanding the Initial Setup:
- A converging lens forms a real image I on its optic axis.
- The image is formed at a distance v from the lens, where v is the image distance.
2. Effect of Introducing the Glass Slab:
- When a glass slab is introduced, it alters the effective optical path due to its refractive index μ and thickness t.
- The light travels slower in the glass slab compared to air, which affects the position of the image.
3. Calculating the Shift in Image Position:
- The optical path length (OPL) in air is given by the distance traveled multiplied by the refractive index of air (which is approximately 1).
- The OPL in the glass slab is given by μ⋅t.
- The effective shift in the image position due to the introduction of the slab can be calculated using the formula:
\(
\text{Shift} = t \left(1 - \frac{1}{\mu}\right)
\)
- This formula accounts for the difference in the optical path length before and after the introduction of the slab.
4. Determining the New Position of Image I':
- The new position of the image I' after the introduction of the slab will be:
\(
I' = I + \text{Shift}
\)
- Therefore, substituting the shift:
\(
I' = I + t \left(1 - \frac{1}{\mu}\right)
\)
5. Conclusion:
- The image I will move closer to the lens by the distance calculated above, resulting in a new image position I'.
- A converging lens forms a real image I on its optic axis.
- The image is formed at a distance v from the lens, where v is the image distance.
- When a glass slab is introduced, it alters the effective optical path due to its refractive index μ and thickness t.
- The light travels slower in the glass slab compared to air, which affects the position of the image.
- The optical path length (OPL) in air is given by the distance traveled multiplied by the refractive index of air (which is approximately 1).
- The OPL in the glass slab is given by μ⋅t.
- The effective shift in the image position due to the introduction of the slab can be calculated using the formula:
\(
\text{Shift} = t \left(1 - \frac{1}{\mu}\right)
\)
- This formula accounts for the difference in the optical path length before and after the introduction of the slab.
- The new position of the image I' after the introduction of the slab will be:
\(
I' = I + \text{Shift}
\)
- Therefore, substituting the shift:
\(
I' = I + t \left(1 - \frac{1}{\mu}\right)
\)
- The image I will move closer to the lens by the distance calculated above, resulting in a new image position I'.
Similar Questions
P is a point on the axis of a concave mirror. The image of P, formed by the mirror, coincides with P. A rectangular glass slab of thickness t and refractive index μ is now introduced between P and the mirror. For the image of P to coincide with P again, the mirror must be moved
View SolutionA parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
View SolutionA parallel beam of light is incident on a lens of focal length 10cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. The nature of the final image from the lens slab combination is: (Assume rays paraxial)
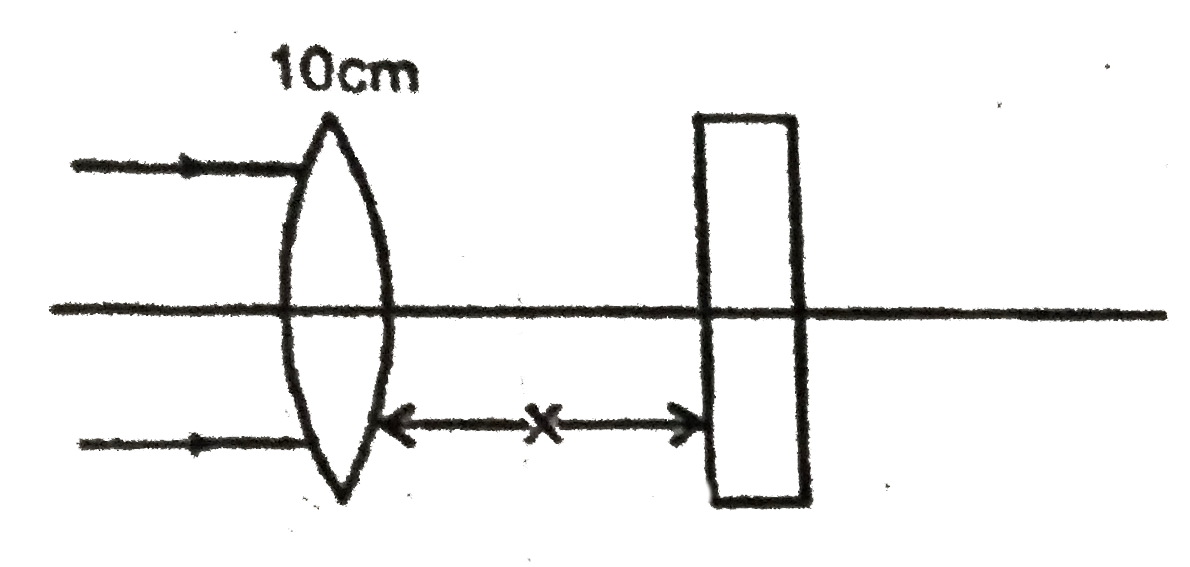
View SolutionA point object is placed at a distance of 25cm from a convex lens. Its focal length is 22cm. A glass slab of refractive index 1.5 is inserted between the lens and the object, then the image is formed at infinity. Find the thickness of the glass slab (in cm).
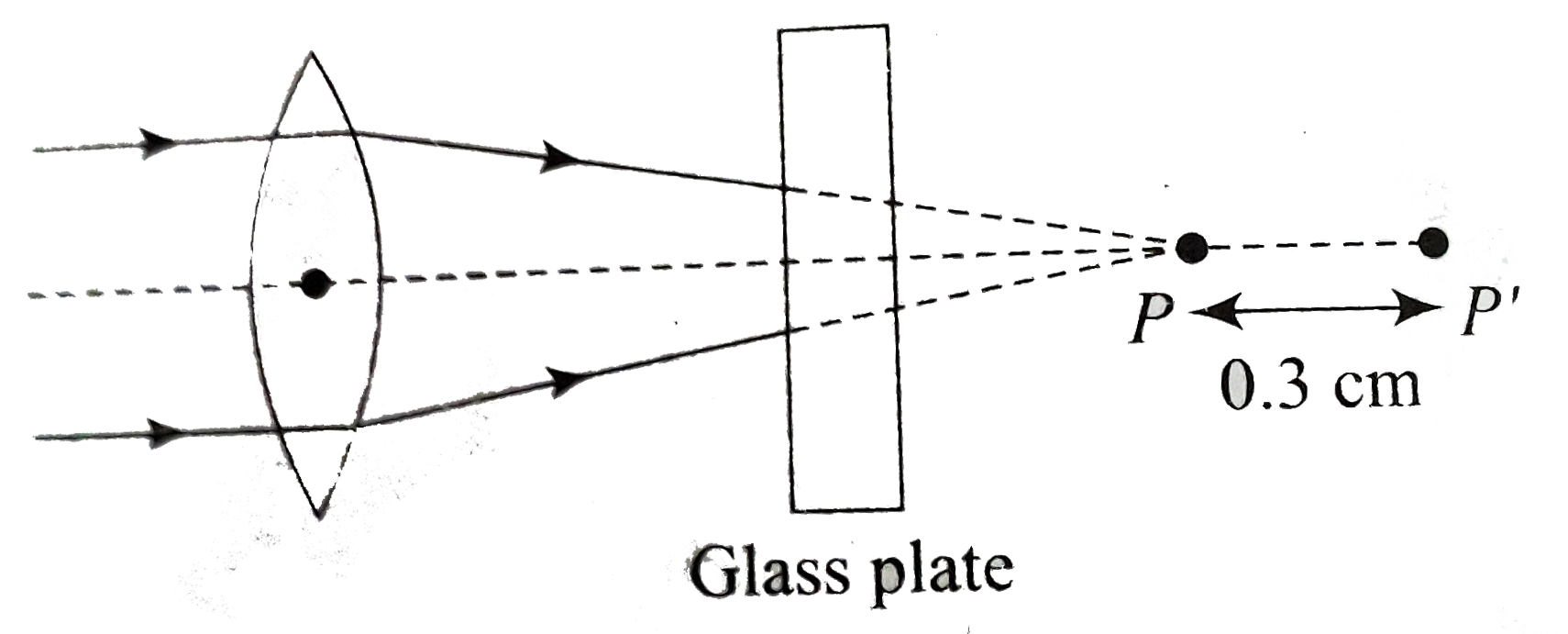
View SolutionRays from a lens are converging toward a point P, a shown in Figure. How much thick glass plate having refractive index 1.6 must be located between the lens and point P, so that the image will be formed at P′?
View SolutionA convex forms a real image of a poinnt object placed on its principal axis. If the upper half of the lens is painted black
View SolutionA biconvex lens of focal length 40 cm is placed in front of an object at a distance of 20 cm . Now a slab of refractive index 43 is placed somewhere in between the lens and the object. The shift in the image formed after the introduction of slab equals (thickness of the slab is 2 mm)
View SolutionWhen an object is placed 60cm in front of a diverging lens, a virtual image is formed 20cm from the lens. The lens is made of a refractive index μ=1.65 and its two spherical surfaces have the same radius of curvature. What is the value of this radius?
View SolutionA thin convex lens L (refractive index =1.5) is placed on a plane mirror M. when a pin is placed at A, such that OA=18 cm, its real inverted image is formed at A itself, as shown in figure. when a liquid of refractive index μi is put between the lens and the mirror, the pin has to be removed to A',. such that OA'=27 cm, to get its inverted real image at A' itself. the value of μi will be

View SolutionA point object is placed at a diatance of 25 cm from a convex lens of focal length 20 cm. If a glass slab of thickness t and refractive index 1.5 is inserted between the lens and the object, the image is formed at infinity. The thickness t is
View Solution
