The dimensions of specific resistance are
[ML2T−2A−1]
[ML3T−3A−2]
[ML3T−2A−1]
[ML2T−2A−2]
The correct Answer is:B
To find the dimensions of specific resistance (also known as resistivity), we start with the formula for resistance R:
R=ρLA
Where:
- R is the resistance,
- ρ is the resistivity (specific resistance),
- L is the length of the conductor,
- A is the cross-sectional area of the conductor.
From this equation, we can express resistivity ρ as:
ρ=R⋅AL
Step 1: Determine the dimensions of resistance R
To find the dimensions of resistance, we can use the formula for heat generated in a resistor:
H=I2RT
Where:
- H is the heat generated,
- I is the current,
- T is the time.
Rearranging gives us:
R=HI2T
Step 2: Find the dimensions of heat H
The dimension of heat can be expressed as:
(H)=ML2T−2
Step 3: Find the dimensions of current I
The dimension of current I (in terms of ampere) is:
(I)=A
Step 4: Find the dimensions of time T
The dimension of time is:
(T)=T
Step 5: Substitute the dimensions into the resistance formula
Now substituting these dimensions into the resistance formula:
(R)=ML2T−2(A2)(T)=ML2T−2A2T=ML2A2T3
Thus, the dimension of resistance R is:
(R)=ML2T−3A−2
Step 6: Substitute into the resistivity formula
Now substituting the dimensions of R back into the resistivity formula:
ρ=R⋅AL
Substituting the dimensions we have:
(ρ)=ML2T−3A−2⋅L2L=ML3T−3A−2
Final Result
Thus, the dimensions of specific resistance (resistivity) are:
(ρ)=ML3T−3A−2
- R is the resistance,
- ρ is the resistivity (specific resistance),
- L is the length of the conductor,
- A is the cross-sectional area of the conductor.
- H is the heat generated,
- I is the current,
- T is the time.
Similar Questions
The dimensions of thermal resistance are
View SolutionDimensions of electrical resistence are
View SolutionWhich of the following combinations has the dimension of electrical resistance (∈0 is the permittivity of vacuum and μ0 is the permeability of vacuum)?
View SolutionWhich of the following combinations has the dimension of electrical resistance (∈0 is the permittivity of vacuum and μ0 is the permeability of vacuum)?
View SolutionTwo wires that are made up of two different materials whose specific resistance are in the ratio 2 : 3, length 3 : 4 and area 4 : 5. The ratio of their resistances is
View SolutionDimension of electrical resistance is :-
View SolutionThe dimensions of a conductor of specific resistance p are shown. Find the resistance of the conductor across AB, CD and EF.
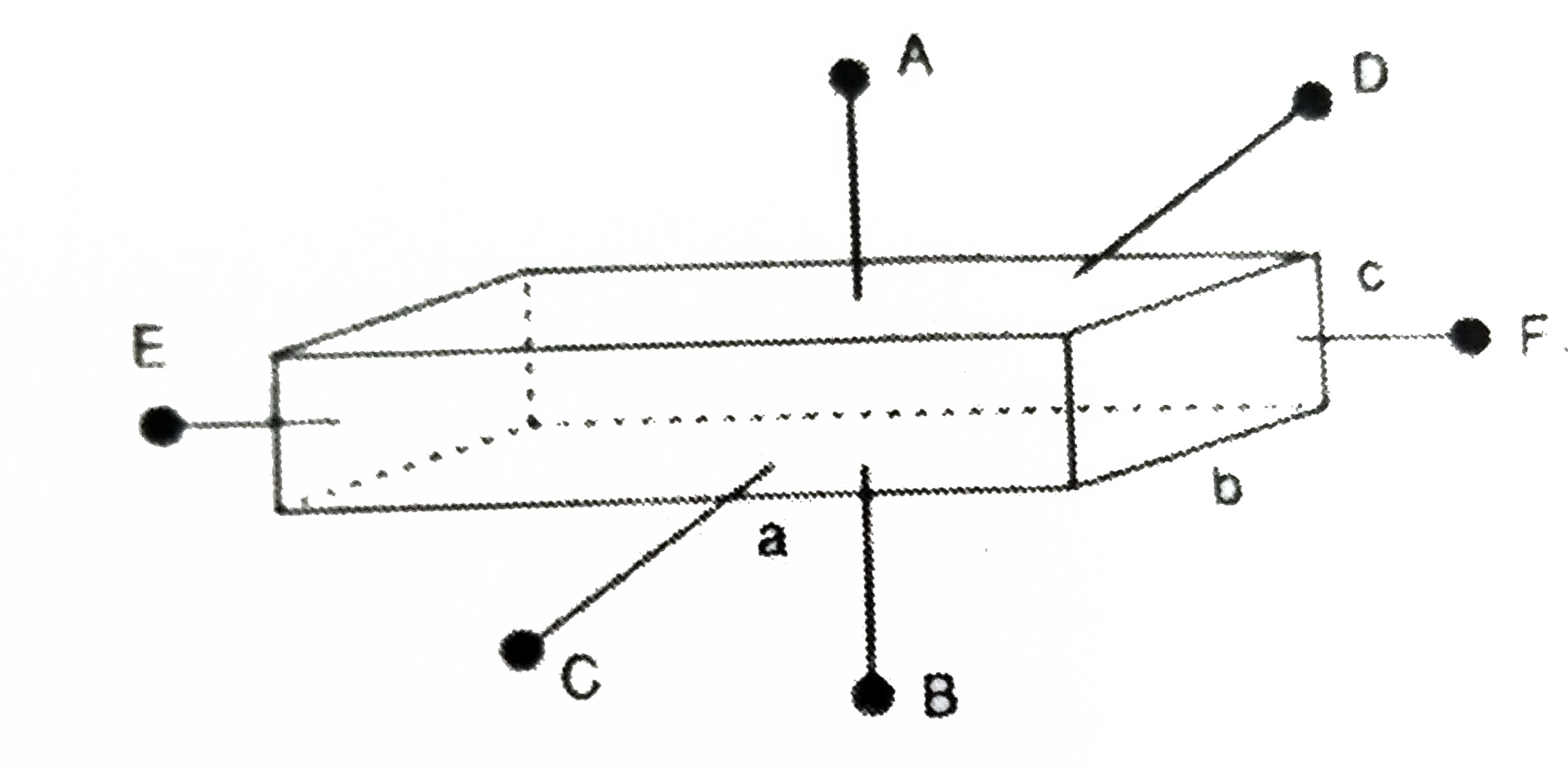
View SolutionState the order of specific resistance of
a semiconductor
View SolutionState the order of specific resistance of
a metal,
View SolutionThe dimension of resistance is
View Solution
