A rocket is fired upward from the earth's surface such that it creates an acceleration of 19.6 m/sec . If after 5 sec its engine is switched off, the maximum height of the rocket from earth's surface would be
245 m
490 m
980 m
735 m
The correct Answer is:A
To solve the problem of finding the maximum height of a rocket fired upward from the Earth's surface, we can break it down into several steps.
1. Identify Given Data:
- Acceleration of the rocket, a=19.6m/s2
- Time of engine firing, t=5s
- Initial velocity, u=0m/s (since the rocket starts from rest)
2. Calculate Final Velocity After 5 Seconds:
We can use the equation of motion:
v=u+at
Substituting the values:
v=0+(19.6m/s2)(5s)=98m/s
3. Calculate the Distance Covered During the First 5 Seconds:
We can use the equation:
x=ut+12at2
Substituting the values:
x=0⋅5+12(19.6m/s2)(5s)2
x=12(19.6)(25)=245m
4. Calculate the Maximum Height After the Engine is Turned Off:
After the engine is turned off, the rocket will continue to rise until its velocity becomes zero. We can use the following equation:
v2=u2−2gh
Here, v=0 (at maximum height), u=98m/s, and g=9.8m/s2. Rearranging for h:
0=(98)2−2(9.8)h
2(9.8)h=(98)2
h=(98)22⋅9.8=960419.6=490m
5. Calculate the Total Maximum Height:
The total height H is the sum of the distance covered during the first 5 seconds and the additional height gained after the engine is turned off:
H=x+h=245m+490m=735m
Final Answer:
The maximum height of the rocket from the Earth's surface is 735 meters.
---
- Acceleration of the rocket, a=19.6m/s2
- Time of engine firing, t=5s
- Initial velocity, u=0m/s (since the rocket starts from rest)
We can use the equation of motion:
v=u+at
Substituting the values:
v=0+(19.6m/s2)(5s)=98m/s
We can use the equation:
x=ut+12at2
Substituting the values:
x=0⋅5+12(19.6m/s2)(5s)2
x=12(19.6)(25)=245m
After the engine is turned off, the rocket will continue to rise until its velocity becomes zero. We can use the following equation:
v2=u2−2gh
Here, v=0 (at maximum height), u=98m/s, and g=9.8m/s2. Rearranging for h:
0=(98)2−2(9.8)h
2(9.8)h=(98)2
h=(98)22⋅9.8=960419.6=490m
The total height H is the sum of the distance covered during the first 5 seconds and the additional height gained after the engine is turned off:
H=x+h=245m+490m=735m
The maximum height of the rocket from the Earth's surface is 735 meters.
Similar Questions
If a ball is thrown upwards from the surface of earth :
View SolutionA rocket is fired with a speed u=3√gR from the earth surface . What will be its speed at interstellar space ?
View SolutionA rocket is launched vertical from the surface of the earth of radius R with an initial speed v. If atmospheric resistance is neglected, then maximum height attained by the rocket is
View SolutionA rocket is fired vertically from the ground. It moves upwards with a constant acceleration 10m/s2 after 30 sec the fuel is finished. After what time from the instant of firing the rocket will attain the maximum height? g=10m/s2:-
View SolutionRocket engines lift a rocket from the earth surface because hot gas with high velocity
View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :
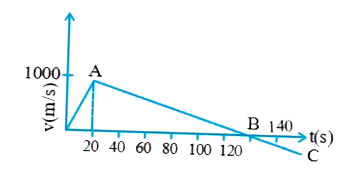
View SolutionA rocket fired from the earth's surface ejects 1% of its mass at a speed of 2000 ms−1 in the first second. Find the average acceleration of the rocket in the first second.
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionA body is projected vertically upwards from the surface of earth with a velocity equal to half the escape velocity. If R be the radius of earth, maximum height attained by the body from the surface of earth is Rn. Find the value of n.
View SolutionA particle is fired vertically upward fom earth's surface and it goes up to a maximum height of 6400 km. find the initial speed of particle.
View Solution
