The dispersive powers of glasses of lenses used in an achromatic pair are in the ratio 5 : 3. If the focal length of the concave lens is 15 cm , then the nature and focal length of the other lens would be
convex, 9 cm
concave, 9 cm
convex, 25 cm
concave, 25 cm
The correct Answer is:A
To solve the problem, we need to determine the nature and focal length of the other lens in an achromatic pair, given the dispersive powers and the focal length of the concave lens.
1. Understand the Relationship:
The dispersive powers (ω) of the lenses in an achromatic pair are related to their focal lengths (f). The relationship is given by:
ω1ω2=f1f2
where:
- ω1 is the dispersive power of the concave lens,
- ω2 is the dispersive power of the other lens,
- f1 is the focal length of the concave lens,
- f2 is the focal length of the other lens.
2. Substitute Given Values:
From the problem, we know:
- The ratio of dispersive powers is 53,
- The focal length of the concave lens f1=−15 cm (negative because it is a concave lens).
Substituting these values into the equation gives:
53=−15f2
3. Cross-Multiply to Solve for f2:
Cross-multiplying gives:
5f2=−45
Now, solving for f2:
f2=−455=−9 cm
4. Determine the Nature of the Lens:
Since f2 is negative, this indicates that the other lens is also a concave lens.
Final Answer:
- The nature of the other lens is concave.
- The focal length of the other lens is -9 cm.
The dispersive powers (ω) of the lenses in an achromatic pair are related to their focal lengths (f). The relationship is given by:
ω1ω2=f1f2
where:
- ω1 is the dispersive power of the concave lens,
- ω2 is the dispersive power of the other lens,
- f1 is the focal length of the concave lens,
- f2 is the focal length of the other lens.
From the problem, we know:
- The ratio of dispersive powers is 53,
- The focal length of the concave lens f1=−15 cm (negative because it is a concave lens).
53=−15f2
Cross-multiplying gives:
5f2=−45
Now, solving for f2:
f2=−455=−9 cm
Since f2 is negative, this indicates that the other lens is also a concave lens.
- The nature of the other lens is concave.
- The focal length of the other lens is -9 cm.
Similar Questions
Find the focal length of the lens used.
View SolutionThe focal length of a plano-concave lens is -10 cm , then its focal length when its palne surface is polished is
View SolutionIf the focal length of the objective lens is increased then Magnifying power
View SolutionIf the focal length of objective lens is increased then magnifying power of
View SolutionTwo lenses are placed in contact with each other and the focal length of combination is 80cm. If the focal length of one is 20cm, then the power of the other will be
View SolutionThe dispersive power of the material of a lens is 0.04 and the focal length of the lens is 10cm. Find the difference in the focal length (in mm) of the lens for violet and red colour.
View SolutionThe figure below shows the positions of a point object 0, two lenses, a plane mirror and the final image I which coincides with the object. The focal length of the convex lens is 20 cm. Calculate the focal length of the concave lens.
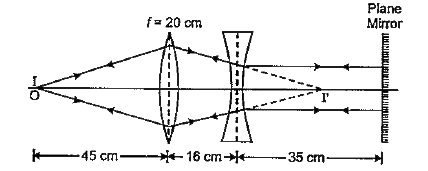
View SolutionThe length of the compound microscope is 14cm. The magnifying power for relaxed eye is 25. If the focal length of eye lens is 5cm, then the object distance for objective lens will be
View SolutionA convex lens of focal length A and a concave lens of focal length B are placed in contact. The focal length of the combination is
View SolutionAn achromatic lens-doublet is formed by placing in contact a convex lens of focal length 20cm and a concave lens of focal length 30cm. The dispersive power of the material of the convex lens is 0.8. Determine the dispersive power of the material of the concave lens. Calculate the focal length of the lens-doublet.
View Solution
