The minimum distance between an object and its real image formed by a thin convex lens of focal length f is K.f. Find the value of K.
3F
4F
32F
2F
To solve the problem of finding the value of K such that the minimum distance between an object and its real image formed by a thin convex lens of focal length f is K⋅f, we can follow these steps:
1. Understanding the Lens Formula:
The lens formula is given by:
1v−1u=1f
where v is the image distance, u is the object distance, and f is the focal length of the lens.
2. Setting Up the Distances:
Let the object distance be u and the image distance be v. According to the problem, the minimum distance between the object and the image is given by:
d=|u|+|v|=K⋅f
Since both distances are positive, we can write:
d=u+v=K⋅f
3. Expressing Image Distance in Terms of Object Distance:
From the lens formula, we can express v in terms of u:
v=ufu−f
4. Substituting into the Distance Equation:
Substitute v into the distance equation:
u+ufu−f=K⋅f
5. Finding a Common Denominator:
To combine the terms, we need a common denominator:
u(u−f)+ufu−f=K⋅f
Simplifying the numerator:
u2−uf+ufu−f=K⋅f
This simplifies to:
u2u−f=K⋅f
6. Rearranging the Equation:
Rearranging gives:
u2=K⋅f(u−f)
Expanding this:
u2=K⋅fu−K⋅f2
Rearranging to form a quadratic equation:
u2−K⋅fu+K⋅f2=0
7. Using the Discriminant:
For u to have real values, the discriminant of this quadratic equation must be non-negative:
D=(Kf)2−4(Kf2)≥0
Simplifying gives:
K2f2−4Kf2≥0
Factoring out f2:
f2(K2−4K)≥0
Since f2>0, we have:
K2−4K≥0
8. Finding the Roots:
Factoring gives:
K(K−4)≥0
The roots are K=0 and K=4. The solution to this inequality is:
K≤0orK≥4
9. Conclusion:
Since K must be positive (as it represents a distance), the minimum value of K is:
K=4
Final Answer:
The value of K is 4.
The lens formula is given by:
1v−1u=1f
where v is the image distance, u is the object distance, and f is the focal length of the lens.
Let the object distance be u and the image distance be v. According to the problem, the minimum distance between the object and the image is given by:
d=|u|+|v|=K⋅f
Since both distances are positive, we can write:
d=u+v=K⋅f
From the lens formula, we can express v in terms of u:
v=ufu−f
Substitute v into the distance equation:
u+ufu−f=K⋅f
To combine the terms, we need a common denominator:
u(u−f)+ufu−f=K⋅f
Simplifying the numerator:
u2−uf+ufu−f=K⋅f
This simplifies to:
u2u−f=K⋅f
Rearranging gives:
u2=K⋅f(u−f)
Expanding this:
u2=K⋅fu−K⋅f2
Rearranging to form a quadratic equation:
u2−K⋅fu+K⋅f2=0
For u to have real values, the discriminant of this quadratic equation must be non-negative:
D=(Kf)2−4(Kf2)≥0
Simplifying gives:
K2f2−4Kf2≥0
Factoring out f2:
f2(K2−4K)≥0
Since f2>0, we have:
K2−4K≥0
Factoring gives:
K(K−4)≥0
The roots are K=0 and K=4. The solution to this inequality is:
K≤0orK≥4
Since K must be positive (as it represents a distance), the minimum value of K is:
K=4
The value of K is 4.
Similar Questions

The distance between a convex lens and a plane mirror is 10 cm. The parallel rays incident on the convex lens after reflection from the mirror forms image at the optical centre of the lens. Focal length of lens will be
View SolutionThe minimum distance between an object and its real image formed by a convex lens is
View SolutionThe minimum distance between a real object and its real image formed by a thin converging lens of focal length f is
View SolutionThe minimum distance between the object and its real image for concave mirror is
View SolutionShown an object and its image formed by a thin lens. Then the nature and focal length of lens is
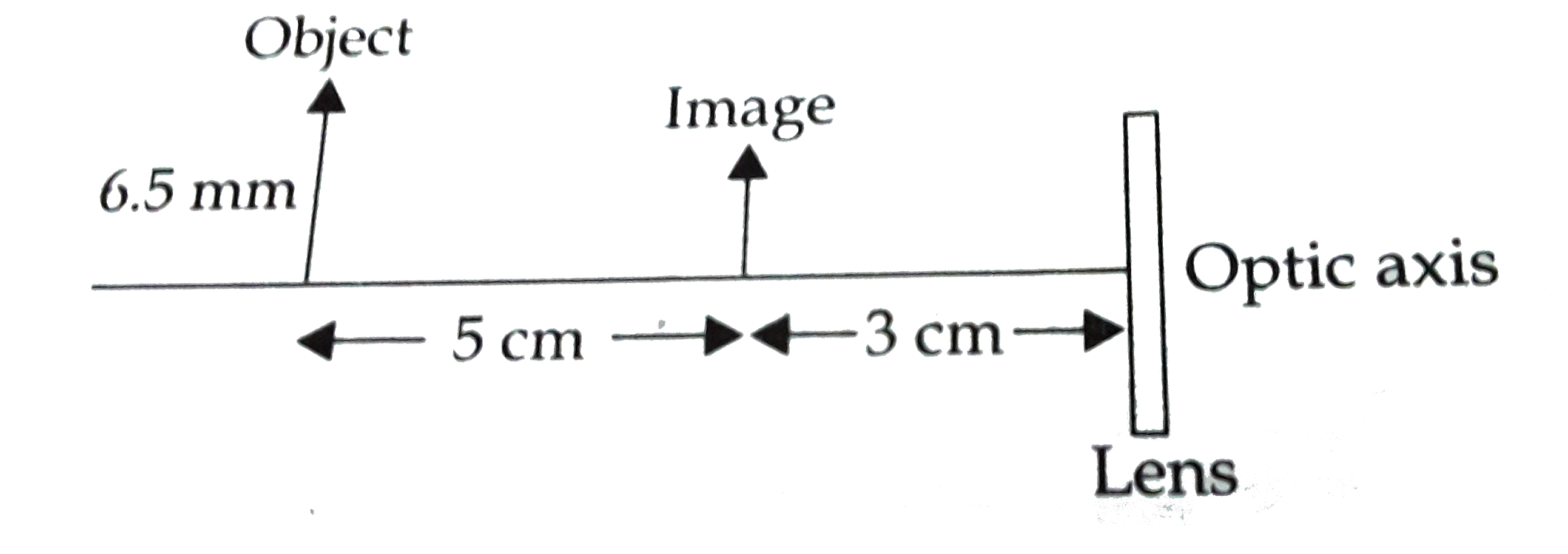
View SolutionIf the distances of an object and its virtual image from the focus of a convex lens of focal length f are 1 cm each, then f is
View SolutionIf the distances of an object and its virtual image from the focus of a convex lens of focal length f are 1 cm each, then f is
View SolutionThe distance between an object and its doubly magnified image by a concave mirror is: [Assume f= focal length]
View SolutionAn object is placed at a distance u from an equiconvex lens such that the distannce between the object and its real image is minimum. The focal length of the lens is f. The value of u is
View SolutionThe distance between the object and its real image from the convex lens is 60 cm and the height of image is two times the height of object . The focal length of the lens is
View Solution
