The minimum distance between a real object and its real image formed by a thin converging lens of focal length f is
4f
2f
f
f/2
The correct Answer is:A
To find the minimum distance between a real object and its real image formed by a thin converging lens of focal length f, we can follow these steps:
Step 1: Understand the Lens Formula
The lens formula relates the object distance u, the image distance v, and the focal length f of the lens:
1f=1v−1u
For a real object, u is negative, and for a real image, v is positive.
Step 2: Express the Distance Between Object and Image
The distance D between the object and the image can be expressed as:
D=v−(−u)=v+u
This simplifies to:
D=v+u
Step 3: Rearrange the Lens Formula
Rearranging the lens formula gives:
1v=1f+1u
This can be rewritten as:
v=ufu+f
Step 4: Substitute v into the Distance Equation
Substituting v into the distance equation gives:
D=ufu+f+u
Now, we can combine the terms:
D=ufu+f+u(u+f)u+f=uf+u2+ufu+f=u2+2ufu+f
Step 5: Differentiate to Find Minimum Distance
To find the minimum distance, we differentiate D with respect to u and set the derivative equal to zero:
dDdu=(2u+2f)(u+f)−(u2+2uf)(u+f)2=0
This simplifies to:
2u2+2uf+2fu+2f2−u2−2uf=0
u2+2f2=0
From this, we can solve for u.
Step 6: Solve for Minimum Distance
Setting the derivative to zero leads to:
u=−2f
Thus, the minimum distance D can be calculated as:
D=v+u=(−2f)f−2f+f−2f=2f
Conclusion
The minimum distance between the real object and its real image formed by a thin converging lens of focal length f is:
2f
The lens formula relates the object distance u, the image distance v, and the focal length f of the lens:
1f=1v−1u
For a real object, u is negative, and for a real image, v is positive.
The distance D between the object and the image can be expressed as:
D=v−(−u)=v+u
This simplifies to:
D=v+u
Rearranging the lens formula gives:
1v=1f+1u
This can be rewritten as:
v=ufu+f
Substituting v into the distance equation gives:
D=ufu+f+u
Now, we can combine the terms:
D=ufu+f+u(u+f)u+f=uf+u2+ufu+f=u2+2ufu+f
To find the minimum distance, we differentiate D with respect to u and set the derivative equal to zero:
dDdu=(2u+2f)(u+f)−(u2+2uf)(u+f)2=0
This simplifies to:
2u2+2uf+2fu+2f2−u2−2uf=0
u2+2f2=0
From this, we can solve for u.
Setting the derivative to zero leads to:
u=−2f
Thus, the minimum distance D can be calculated as:
D=v+u=(−2f)f−2f+f−2f=2f
The minimum distance between the real object and its real image formed by a thin converging lens of focal length f is:
2f
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
62 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-3
80 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Problem
33 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
The minimum distance between an object and its real image formed by a thin convex lens of focal length f is K.f. Find the value of K.
View Solution
The distance between a convex lens and a plane mirror is 10 cm. The parallel rays incident on the convex lens after reflection from the mirror forms image at the optical centre of the lens. Focal length of lens will be
View SolutionThe minimum distance between an object and its real image formed by a convex lens is
View SolutionThe minimum distance between the object and its real image for concave mirror is
View SolutionChoose the correct alternative corresponding to the object distance 'u', image distance 'v' and the focal length 'F' of a converging lens from the following .
(i) The average speed of the image as the object moves with the uniform speed from distance 3F4 to F2 is greater than the average speed of the image as the object moves with same speed from distance F2toF4
(ii) The minimum distance between a real object and its real image in case of a converging lens is 4F where F is its focal length.
View SolutionShown an object and its image formed by a thin lens. Then the nature and focal length of lens is
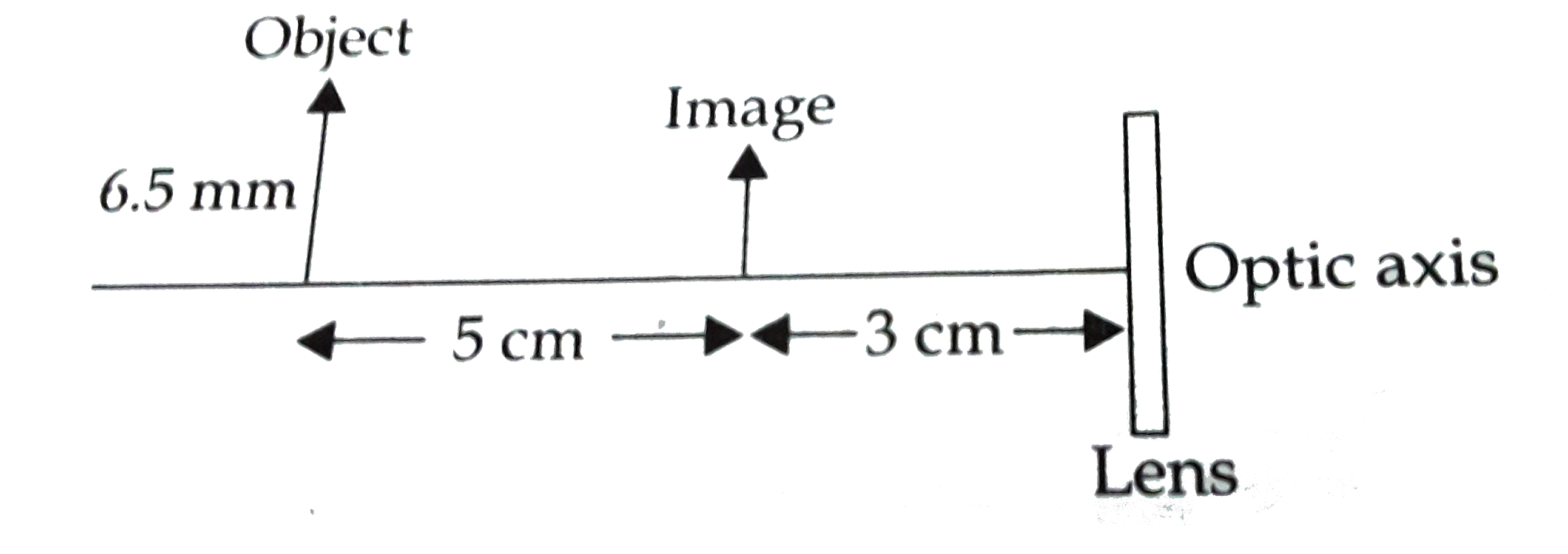
View SolutionChoose the following statement a True of False.
a. The real image formed by a lens is always inverted.
b. The image formed by a lens is always inverted.
c. The image formed by a concave lens is always erect and diminished.
d. An air bubble inside water acts like a concave lens.
e. The distance between a real object and its real image formed by a single lens cannot be more than 4f.
f. I an object is moved at a constant speed toward a convex lens from infinity to focus, then its image moves slower in the begninning and faster later on, away from the lens.
g. The focal length of a glass (μ=1.5) lens is 10 cm in air. When it is completely immersed in water its focal length will become 40cm.
View SolutionThe distance between an object and its doubly magnified image by a concave mirror is: [Assume f= focal length]
View SolutionThe distance between the object and its real image from the convex lens is 60 cm and the height of image is two times the height of object . The focal length of the lens is
View SolutionAssertion: Minimum distance between object and its real image by a convex lens is 4f.
Reason: If object distance from a convex lens is 2f, then its image distace is also 2f.
View Solution
