A toroid with mean radius r0, diameter 2a have N turns carrying current l. What is the magnetic field B inside the the toroid?
NI2πr0
Nl2π(r0+a)
Nlπ(r0+a)
zero
To find the magnetic field B inside a toroid, we can use Ampere's Law, which states that the line integral of the magnetic field around a closed loop is equal to the permeability of free space times the total current passing through the loop.
1. Identify the Parameters:
- Mean radius of the toroid, r0.
- Diameter of the toroid, 2a (thus, the radius a).
- Number of turns, N.
- Current flowing through the wire, I.
2. Draw the Toroid:
- Visualize or sketch the toroid. It is a doughnut-shaped object with a circular cross-section. The mean radius is the average distance from the center of the toroid to the wire.
3. Apply Ampere's Law:
- According to Ampere's Law:
∮B⋅dl=μ0Ienc
- Here, Ienc is the total current enclosed by the loop.
4. Calculate the Line Integral:
- The magnetic field B inside the toroid is assumed to be uniform along the circular path at mean radius r0.
- The differential length dl around the circular path is 2πr0.
- Therefore, the left side of Ampere's Law becomes:
B⋅(2πr0)
5. Determine the Enclosed Current:
- The total current enclosed by the loop is N⋅I (since there are N turns, each carrying current I).
- Thus, the right side of Ampere's Law is:
μ0(N⋅I)
6. Set Up the Equation:
- Equating both sides from Ampere's Law:
B⋅(2πr0)=μ0(N⋅I)
7. Solve for B:
- Rearranging the equation to solve for B:
B=μ0(N⋅I)2πr0
8. Final Expression:
- Therefore, the magnetic field inside the toroid is given by:
B=μ0NI2πr0
- Mean radius of the toroid, r0.
- Diameter of the toroid, 2a (thus, the radius a).
- Number of turns, N.
- Current flowing through the wire, I.
- Visualize or sketch the toroid. It is a doughnut-shaped object with a circular cross-section. The mean radius is the average distance from the center of the toroid to the wire.
- According to Ampere's Law:
∮B⋅dl=μ0Ienc
- Here, Ienc is the total current enclosed by the loop.
- The magnetic field B inside the toroid is assumed to be uniform along the circular path at mean radius r0.
- The differential length dl around the circular path is 2πr0.
- Therefore, the left side of Ampere's Law becomes:
B⋅(2πr0)
- The total current enclosed by the loop is N⋅I (since there are N turns, each carrying current I).
- Thus, the right side of Ampere's Law is:
μ0(N⋅I)
- Equating both sides from Ampere's Law:
B⋅(2πr0)=μ0(N⋅I)
- Rearranging the equation to solve for B:
B=μ0(N⋅I)2πr0
- Therefore, the magnetic field inside the toroid is given by:
B=μ0NI2πr0
Similar Questions
Knowledge Check
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3T
(a) Using Biot-Savart's law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop.
(b) What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show the magnetic field in the open space inside and exterior to the toroid is Zero.
View SolutionA solenoid of length 0⋅5m has a radius of 1cm and is made up of 500 turns. It carries a current of 5A. What is the magnitude of the magnetic field inside the solenoid?
View SolutionA toroid of non ferromagnetic has core of inner radius 25cm and outer radius 26cm. it has 3500 turns & carries a current of 11A, then find the magnetic field at a point
i) In the internal cavity of toroid
ii) At the midpoint of the windings
iii) At a point which is at a distance of 30cm from the centre of toroid
View SolutionA thin solenoid of length 0.4m and having 500 turns of wire carries a current 1A,then find the magnetic field on the axis inside the solenoid.
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
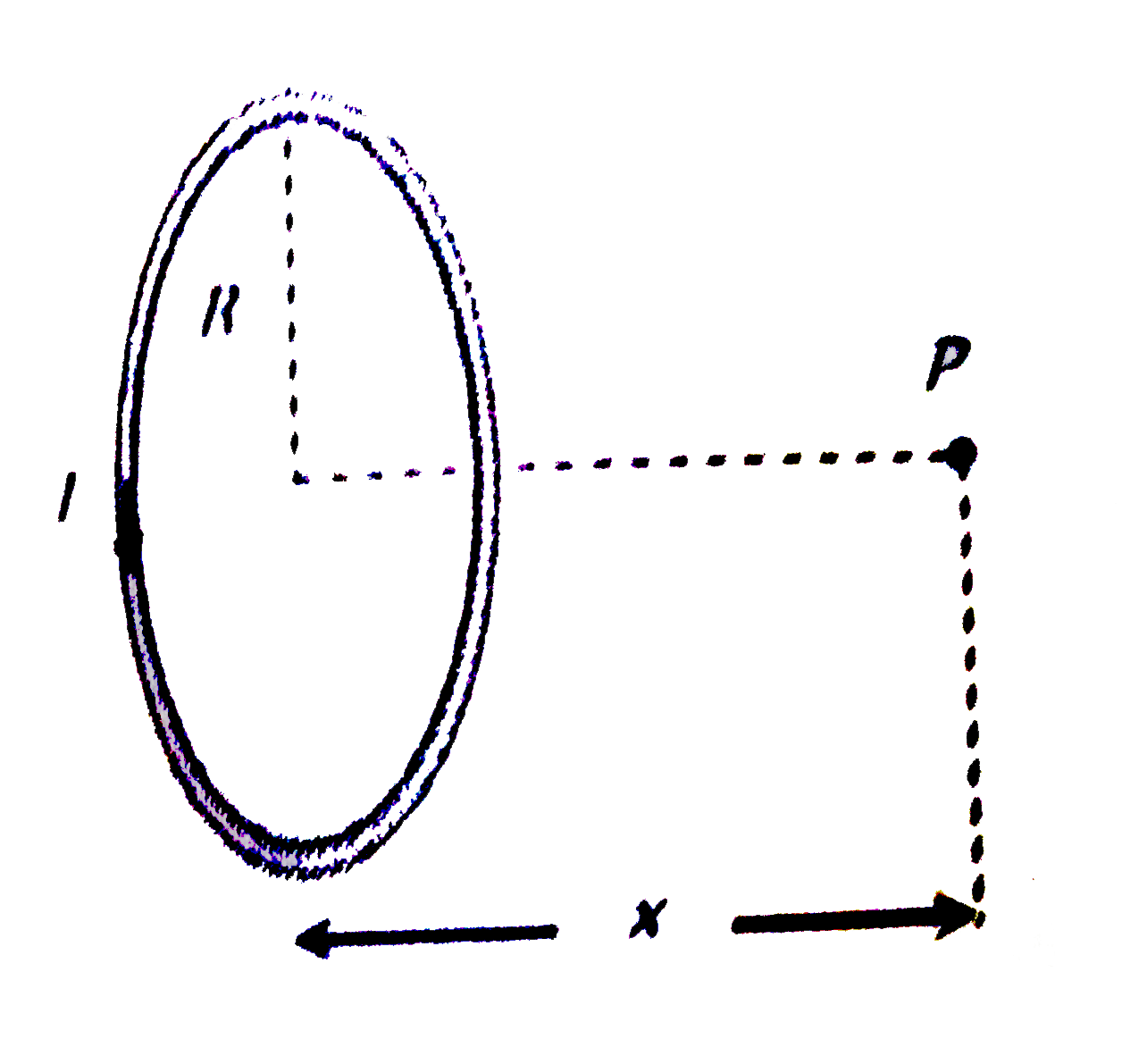
View SolutionA tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View SolutionThe average radius of an air cored made toroid is 0.1 m and it has 500 turns. If it carries 0.5 ampere current, then the magnetic field inside it is :
View Solution
