(a) Using Biot-Savart's law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop.
(b) What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show the magnetic field in the open space inside and exterior to the toroid is Zero.
Solution:
(a) Deriving the expression for the magnetic field at a point on the axis of a circular current loop using Biot-Savart's Law:
1. Understanding the Setup:
- Consider a circular current loop of radius r carrying a current I.
- We want to find the magnetic field B at a point P located on the axis of the loop at a distance d from the center of the loop.
2. Applying Biot-Savart's Law:
- According to Biot-Savart's Law, the magnetic field dB due to a small current element dl is given by:
dB=μ0I4πdl×^rr2
- Here, ^r is the unit vector pointing from the current element to the point P, and r is the distance from the current element to the point P.
3. Finding dl and ^r:
- The current element dl is tangential to the loop and can be expressed as dl=rdθ^ϕ, where ^ϕ is the unit vector in the direction of the current.
- The distance R from the current element to point P can be expressed using the Pythagorean theorem:
R=√r2+d2
4. Calculating dB:
- The angle θ between dl and ^r is given by:
cosθ=dR
- Therefore, the magnetic field contribution dB can be simplified to:
dB=μ0I4πdlR2cosθ
- Substituting cosθ:
dB=μ0I4πdl(r2+d2)3/2d
5. Integrating Around the Loop:
- To find the total magnetic field B, integrate dB around the entire loop:
B=∫dB=∫μ0Idl⋅d(r2+d2)3/2
- The total length of the loop is 2πr, thus:
B=μ0Id(r2+d2)3/2⋅2πr
6. Final Expression:
- The magnetic field at point P on the axis of the circular loop is:
B=μ0I2r⋅d(r2+d2)3/2
(b) Understanding a Toroid and Finding the Magnetic Field:
1. Definition of a Toroid:
- A toroid is a solenoid bent into a circular shape, forming a closed loop. It consists of N turns of wire wound around a circular core.
2. Finding the Magnetic Field Inside the Toroid:
- For a toroid with N turns, average radius r, and carrying a current I, we apply Ampere's Law:
∮B⋅dl=μ0Ienc
- The enclosed current Ienc for N turns is NI.
3. Calculating the Magnetic Field:
- The path of integration is a circle of radius r:
B⋅2πr=μ0NI
- Therefore, the magnetic field B inside the toroid is:
B=μ0NI2πr
4. Magnetic Field in Open Space Inside and Exterior to the Toroid:
- Inside the Toroid: The magnetic field is non-zero as derived above.
- In Open Space Inside the Toroid: No current flows through the Amperian loop, so:
B=0
- Exterior to the Toroid: The net current entering and leaving the plane cancels out, leading to:
B=0
- Consider a circular current loop of radius r carrying a current I.
- We want to find the magnetic field B at a point P located on the axis of the loop at a distance d from the center of the loop.
- According to Biot-Savart's Law, the magnetic field dB due to a small current element dl is given by:
dB=μ0I4πdl×^rr2
- Here, ^r is the unit vector pointing from the current element to the point P, and r is the distance from the current element to the point P.
- The current element dl is tangential to the loop and can be expressed as dl=rdθ^ϕ, where ^ϕ is the unit vector in the direction of the current.
- The distance R from the current element to point P can be expressed using the Pythagorean theorem:
R=√r2+d2
- The angle θ between dl and ^r is given by:
cosθ=dR
- Therefore, the magnetic field contribution dB can be simplified to:
dB=μ0I4πdlR2cosθ
- Substituting cosθ:
dB=μ0I4πdl(r2+d2)3/2d
- To find the total magnetic field B, integrate dB around the entire loop:
B=∫dB=∫μ0Idl⋅d(r2+d2)3/2
- The total length of the loop is 2πr, thus:
B=μ0Id(r2+d2)3/2⋅2πr
- The magnetic field at point P on the axis of the circular loop is:
B=μ0I2r⋅d(r2+d2)3/2
- A toroid is a solenoid bent into a circular shape, forming a closed loop. It consists of N turns of wire wound around a circular core.
- For a toroid with N turns, average radius r, and carrying a current I, we apply Ampere's Law:
∮B⋅dl=μ0Ienc
- The enclosed current Ienc for N turns is NI.
- The path of integration is a circle of radius r:
B⋅2πr=μ0NI
- Therefore, the magnetic field B inside the toroid is:
B=μ0NI2πr
- Inside the Toroid: The magnetic field is non-zero as derived above.
- In Open Space Inside the Toroid: No current flows through the Amperian loop, so:
B=0
- Exterior to the Toroid: The net current entering and leaving the plane cancels out, leading to:
B=0
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set- II]
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
A circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionA toroid having 200 turns carries a current of 1A. The average radius of the toroid is 10 cm. the magnetic field at any point in the open space inside the toroid is
View SolutionUsing Ampere.s Circuital Law, derive an expression for the magnetic field along the axis of a toroidal solenoid.
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
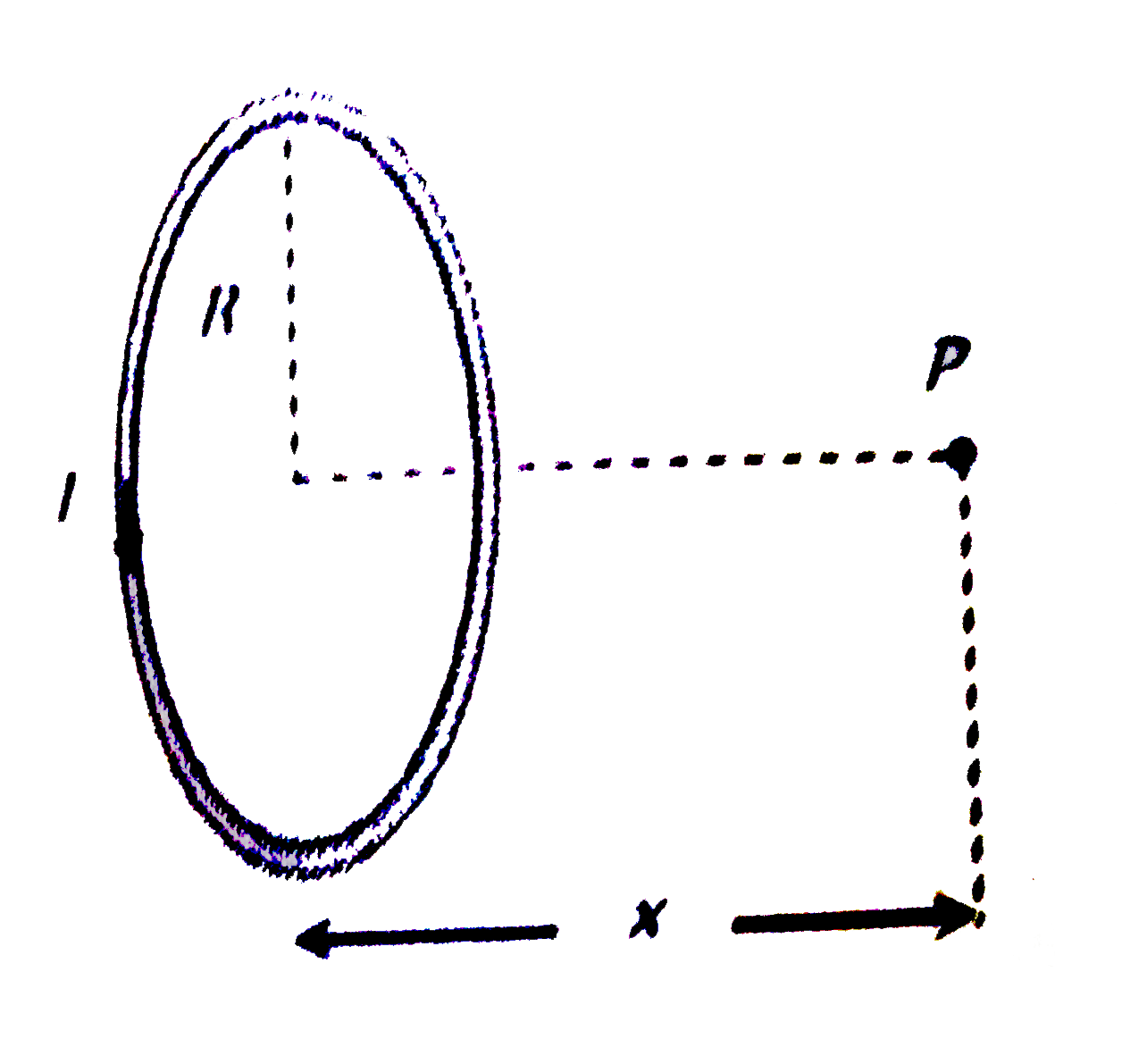
View SolutionA long copper tube of inner radius R carriers a current i. The magnetic field B inside the tube is
View SolutionObtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
View SolutionObtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I.
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionA toroid with mean radius r0, diameter 2a have N turns carrying current l. What is the magnetic field B inside the the toroid?
View Solution
