A particle moving about its equilibrium position with eqaution y=−ax−bt. Interpret the condition
It will always perform the SHM.
It can never perform the SHM.
It can perform SHM only when t>bxa
It can perform SHM only when t≤bxa.
To solve the problem, we need to analyze the motion described by the equation y=−ax−bt and interpret the conditions related to the motion of the particle about its equilibrium position.
1. Understanding the Equation:
The equation given is y=−ax−bt. Here, y represents the position of the particle, x is another variable (which could represent displacement), a and b are constants, and t is time.
2. Differentiating the Equation:
To understand the motion, we first differentiate y with respect to time t:
dydt=−adxdt−b
This equation gives us the velocity of the particle in terms of the rate of change of x with respect to time and the constant b.
3. Second Differentiation:
Next, we differentiate again to find the acceleration:
d2ydt2=−ad2xdt2−0
This simplifies to:
d2ydt2=−ad2xdt2
4. Rearranging the Equation:
Rearranging the equation gives us:
d2ydt2+ad2xdt2=0
5. Interpreting the Result:
The equation derived, d2ydt2+ad2xdt2=0, indicates that the motion described does not conform to the standard form of simple harmonic motion (SHM), which typically has a form like d2ydt2+ω2y=0.
6. Conclusion:
Since the derived equation does not represent SHM, we conclude that the particle cannot perform simple harmonic motion. Therefore, the interpretation of the condition is that the motion described by the equation y=−ax−bt does not lead to SHM.
Final Interpretation:
The particle described by the equation y=−ax−bt does not exhibit simple harmonic motion due to the absence of a restoring force proportional to displacement from an equilibrium position.
The equation given is y=−ax−bt. Here, y represents the position of the particle, x is another variable (which could represent displacement), a and b are constants, and t is time.
To understand the motion, we first differentiate y with respect to time t:
dydt=−adxdt−b
This equation gives us the velocity of the particle in terms of the rate of change of x with respect to time and the constant b.
Next, we differentiate again to find the acceleration:
d2ydt2=−ad2xdt2−0
This simplifies to:
d2ydt2=−ad2xdt2
Rearranging the equation gives us:
d2ydt2+ad2xdt2=0
The equation derived, d2ydt2+ad2xdt2=0, indicates that the motion described does not conform to the standard form of simple harmonic motion (SHM), which typically has a form like d2ydt2+ω2y=0.
Since the derived equation does not represent SHM, we conclude that the particle cannot perform simple harmonic motion. Therefore, the interpretation of the condition is that the motion described by the equation y=−ax−bt does not lead to SHM.
The particle described by the equation y=−ax−bt does not exhibit simple harmonic motion due to the absence of a restoring force proportional to displacement from an equilibrium position.
Similar Questions
Knowledge Check
A charged particle oscillates about its mean equilibrium position with a frequency of 109 Hz. The frequency of electromagnetic waves produced by the oscillator is
A106HzB107HzC108HzD109HzThe particles of a medium oscillate about their equilibrium position, whenever a wave travels through that medium. The phase difference between the oscillations of two such practices varies
Awith time but not with distance separating themBwith distance separation them but not with timeCwith distance separating them as well as with timeDneither with distance separating them nor with time
A charged particle oscillates about its mean equilibrium position with a frerquency of 109Hz. The electromagnetic waves produced.
View SolutionA partical of mass m is moving along the x-axis under the potential V(x)=kx22+λ Where k and x are positive constants of appropriate dimensions . The particle is slightly displaced from its equilibrium position . The particle oscillates with the the angular frequency (ω) given by
View SolutionA particle of mass 2kg is moving of a straight line under the action of force F=(8−2x)N. It is released at rest from x=6m.
a. Is the particle moving simple harmonically.
b. Find the equilibrium position of the particle.
c. Write the equation of motion of the particle.
d. Find the time period of SHM.
View SolutionTwo particles A and B are performing SHM along x and y-axis respectively with equal amplitude and frequency of 2cm and 1Hz respectively. Equilibrium positions of the particles A and B are at the coordinates [3cm,0] and (0,4cm) respectively. At t=0,B is at its equilibrium position and moving towards the origin, while A is nearest to the origin and moving away from the origin-
Equation of motion of particle B can be written as-
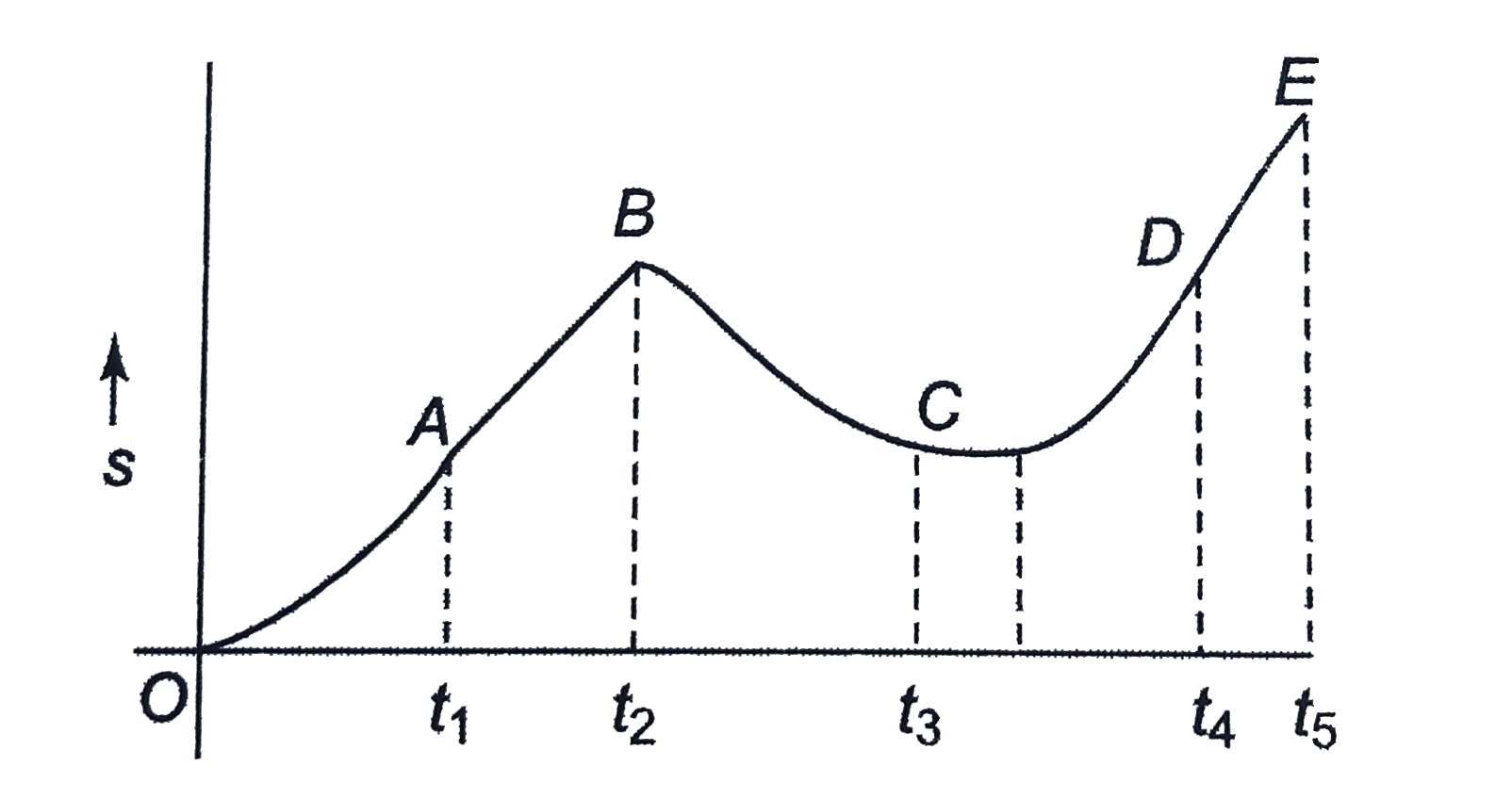
View SolutionA particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
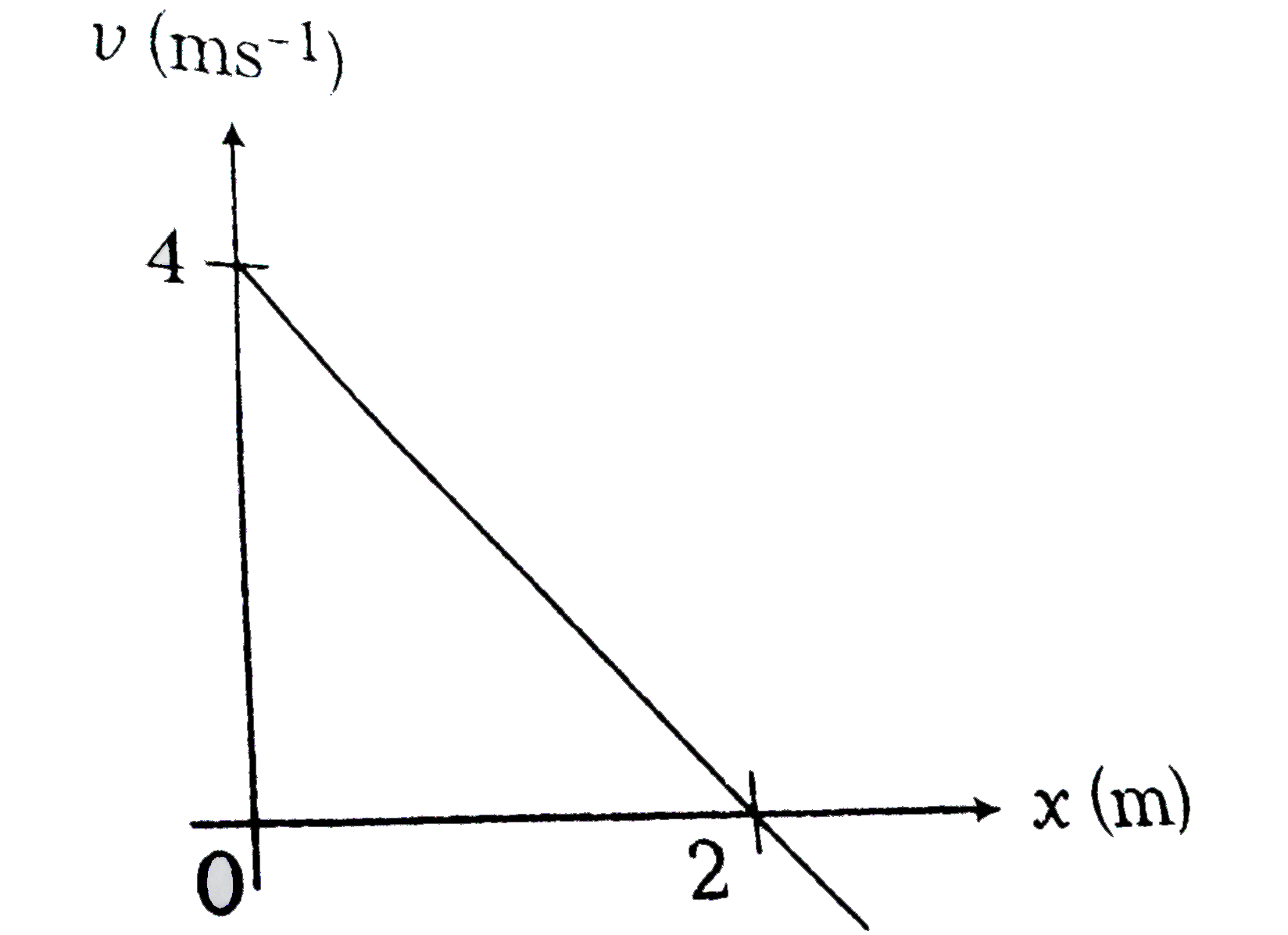
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
View Solution
