A needle of length l m and mass m kg is placed horizontal on wter surface habing surface tension T Find T in terms of m, l (g acceleration due to gravity)
T=mg2l
T=mgl
T=3mg2l
T=m2l
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the needle placed horizontally on the surface of the water due to surface tension.
1. Identify the Forces Acting on the Needle:
- The needle has a weight mg acting downwards due to gravity, where m is the mass of the needle and g is the acceleration due to gravity.
- The surface tension T acts along the surface of the water at both ends of the needle. Since the needle is horizontal, the surface tension will have a vertical component that helps balance the weight of the needle.
2. Determine the Components of Surface Tension:
- The surface tension acts at an angle θ with respect to the horizontal. The vertical component of the surface tension at each end of the needle can be expressed as Tsin(θ).
- Since there are two ends of the needle, the total upward force due to surface tension is 2Tsin(θ).
3. Set Up the Force Balance Equation:
- For the needle to be in equilibrium, the total upward force due to surface tension must equal the downward gravitational force:
2Tsin(θ)=mg
4. Approximate for Small Angles:
- If the angle θ is very small (which is often the case for a needle floating on water), we can use the approximation sin(θ)≈θ and cos(θ)≈1.
- Therefore, we can rewrite the equation as:
2Tθ=mg
5. Relate the Angle to the Length of the Needle:
- The angle θ can be approximated as the ratio of the length of the needle l to the distance from the center of the needle to the surface (which is negligible for our calculations). Thus, we can consider θ as lL where L is some characteristic length (but for simplicity, we can assume it to be negligible).
- However, since we are looking for T in terms of m, l, and g, we can directly relate:
θ≈1(as θ approaches 0)
6. Solve for Surface Tension T:
- Rearranging the equation gives:
T=mg2θ
- Substituting θ≈1:
T=mg2l
Final Result:
Thus, the surface tension T in terms of m, l, and g is:
T=mg2l
- The needle has a weight mg acting downwards due to gravity, where m is the mass of the needle and g is the acceleration due to gravity.
- The surface tension T acts along the surface of the water at both ends of the needle. Since the needle is horizontal, the surface tension will have a vertical component that helps balance the weight of the needle.
- The surface tension acts at an angle θ with respect to the horizontal. The vertical component of the surface tension at each end of the needle can be expressed as Tsin(θ).
- Since there are two ends of the needle, the total upward force due to surface tension is 2Tsin(θ).
- For the needle to be in equilibrium, the total upward force due to surface tension must equal the downward gravitational force:
2Tsin(θ)=mg
- If the angle θ is very small (which is often the case for a needle floating on water), we can use the approximation sin(θ)≈θ and cos(θ)≈1.
- Therefore, we can rewrite the equation as:
2Tθ=mg
- The angle θ can be approximated as the ratio of the length of the needle l to the distance from the center of the needle to the surface (which is negligible for our calculations). Thus, we can consider θ as lL where L is some characteristic length (but for simplicity, we can assume it to be negligible).
- However, since we are looking for T in terms of m, l, and g, we can directly relate:
θ≈1(as θ approaches 0)
- Rearranging the equation gives:
T=mg2θ
- Substituting θ≈1:
T=mg2l
Thus, the surface tension T in terms of m, l, and g is:
T=mg2l
Similar Questions
A wedge of mass m is placed on a smooth fixed horizontal surface and block of mass m is placed on smoth inclined surface of wedfe as shown. The system is then released from rest. (g is acceleration due to gravity)

Select correct option(s)
View SolutionA point mass m, is placed at the surface of a hypothetical planet where acceleration due to gravity is g2, where g acceleration due to gravity at the poles the planet. The latitude of that position is [T is time period of planet rotation about its own axis and R is radius of planet]
View SolutionA satellite of mass m is orbiting the earth (of radius R) at a height h from its surface. The total energy of the satellite in terms of g0, the value of acceleration due to gravity at the earth's surface,
View SolutionA satellite of mass m is orbiting the earth (of radius R) at a height h from its surface. The total energy of the satellite in terms of g0, the value of acceleration due to gravity at the earth's surface is
View SolutionA uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionA particle of mass 'm' is raised to a height h=R from the surface of earth. Find increase in potential energy. R= radius of earth. g= acceleration due to gravity on the surface of earth.
View SolutionTwo masses m and m' are tied with a thread passing over a pulley, m' is on a frictionless horizontal surface and m is hanging freely. If acceleration due to gravity is g, the acceleration of m' in this arrangment will be :
View SolutionA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
View SolutionHow does the time period (T) of a simple pendulum depend on its length (l)? Draw a graph showing the variation of T2 with l. How will you use this graph to determine the value of g (acceleration due to gravity) ?
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
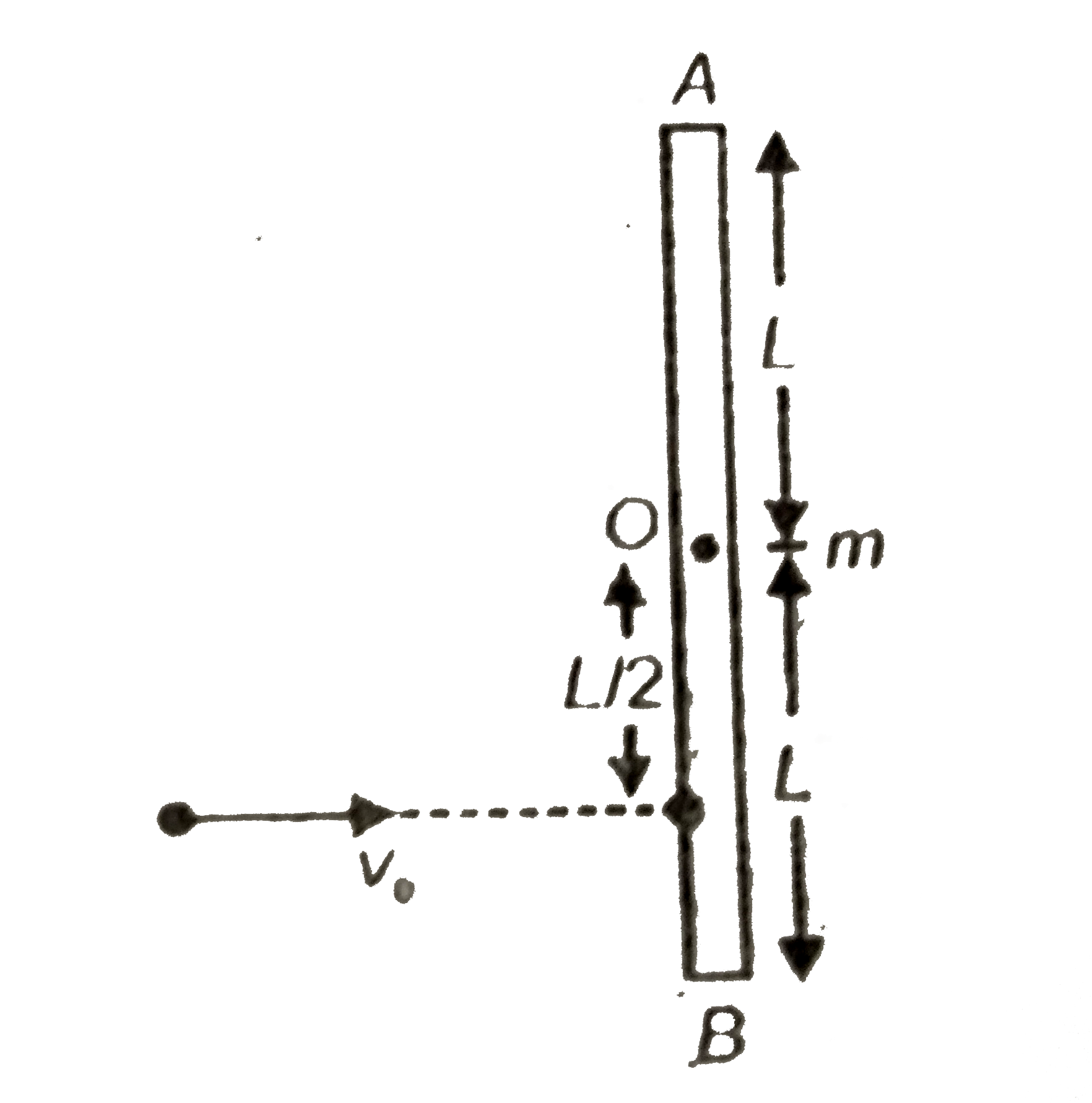
Angular velocity of rod just after collision is
View Solution
