If n inductor of inductance L, radius r, current charges from 10 to I2. Find work done.
To find the work done when the current in n inductors changes from I0 to I2, we can follow these steps:
Step 1: Understand the energy stored in an inductor
The energy U stored in an inductor with inductance L and current I is given by the formula:
U=12LI2
Step 2: Calculate the initial and final energy
- The initial energy U1 when the current is I0:
U1=12LI20
- The final energy U2 when the current is I2:
U2=12LI22
Step 3: Find the change in energy
The work done W is equal to the change in energy, which can be expressed as:
W=U2−U1
Step 4: Substitute the values of U1 and U2
Substituting the expressions for U1 and U2 into the equation for work done:
W=(12LI22)−(12LI20)
Step 5: Factor out common terms
Factoring out the common terms gives:
W=12L(I22−I20)
Final Answer
Thus, the work done when the current changes from I0 to I2 is:
W=12L(I22−I20)
---
The energy U stored in an inductor with inductance L and current I is given by the formula:
U=12LI2
- The initial energy U1 when the current is I0:
U1=12LI20
- The final energy U2 when the current is I2:
U2=12LI22
The work done W is equal to the change in energy, which can be expressed as:
W=U2−U1
Substituting the expressions for U1 and U2 into the equation for work done:
W=(12LI22)−(12LI20)
Factoring out the common terms gives:
W=12L(I22−I20)
Thus, the work done when the current changes from I0 to I2 is:
W=12L(I22−I20)
Similar Questions
Knowledge Check
In an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
A4sB3sC2sD1sIn an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
A4sB3sC2sD1sA condenser of capacity C is charged to a potential difference of V1. The plates of the condenser are then connected to an ideal inductor of inductance L. The current through the inductor when the potential difference across the condenser reduces to V2 is
A(C(V1−V2)2L)12BC(V21−V22)LCC(V21+V22)LD(C(V21−V22)L)12
The inductors of self inductance L1 and L2 are put in series .
View SolutionA condenser of capacity C is charged to a potential difference of V1. The plates of the condenser are then connected to an ideal inductor of inductance L. The current through the inductor wehnn the potential difference across the condenser reduces to V2 is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
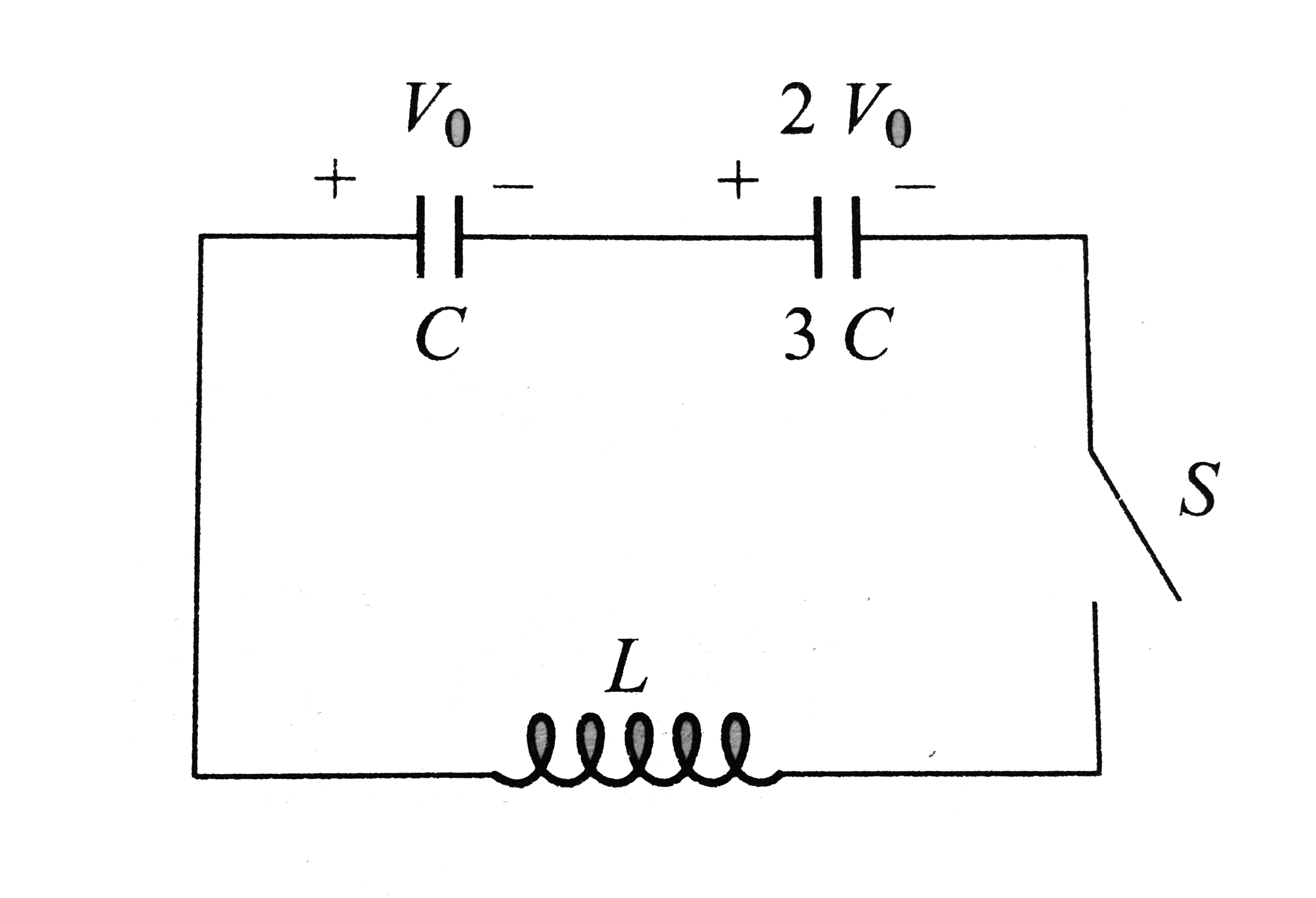
The maximum current in the inductor is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum is
View Solution
