In an inductor of inductance L=100mH, a current of I=10A is flowing. The energy stored in the inductor is
5 J
10 J
100 J
1000 J
The correct Answer is:A
To find the energy stored in an inductor, we can use the formula:
U=12LI2
where:
- U is the energy stored in the inductor,
- L is the inductance of the inductor,
- I is the current flowing through the inductor.
1. Identify the values given in the problem:
- Inductance L=100mH=100×10−3H=0.1H
- Current I=10A
2. Substitute the values into the energy formula:
U=12LI2
U=12×0.1H×(10A)2
3. Calculate I2:
I2=(10A)2=100A2
4. Now substitute I2 back into the equation:
U=12×0.1H×100A2
5. Perform the multiplication:
U=12×10H⋅A2=5J
6. Conclusion:
The energy stored in the inductor is 5J.
Final Answer:
The energy stored in the inductor is 5 joules.
- U is the energy stored in the inductor,
- L is the inductance of the inductor,
- I is the current flowing through the inductor.
- Inductance L=100mH=100×10−3H=0.1H
- Current I=10A
U=12LI2
U=12×0.1H×(10A)2
I2=(10A)2=100A2
U=12×0.1H×100A2
U=12×10H⋅A2=5J
The energy stored in the inductor is 5J.
The energy stored in the inductor is 5 joules.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example
71 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Two capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
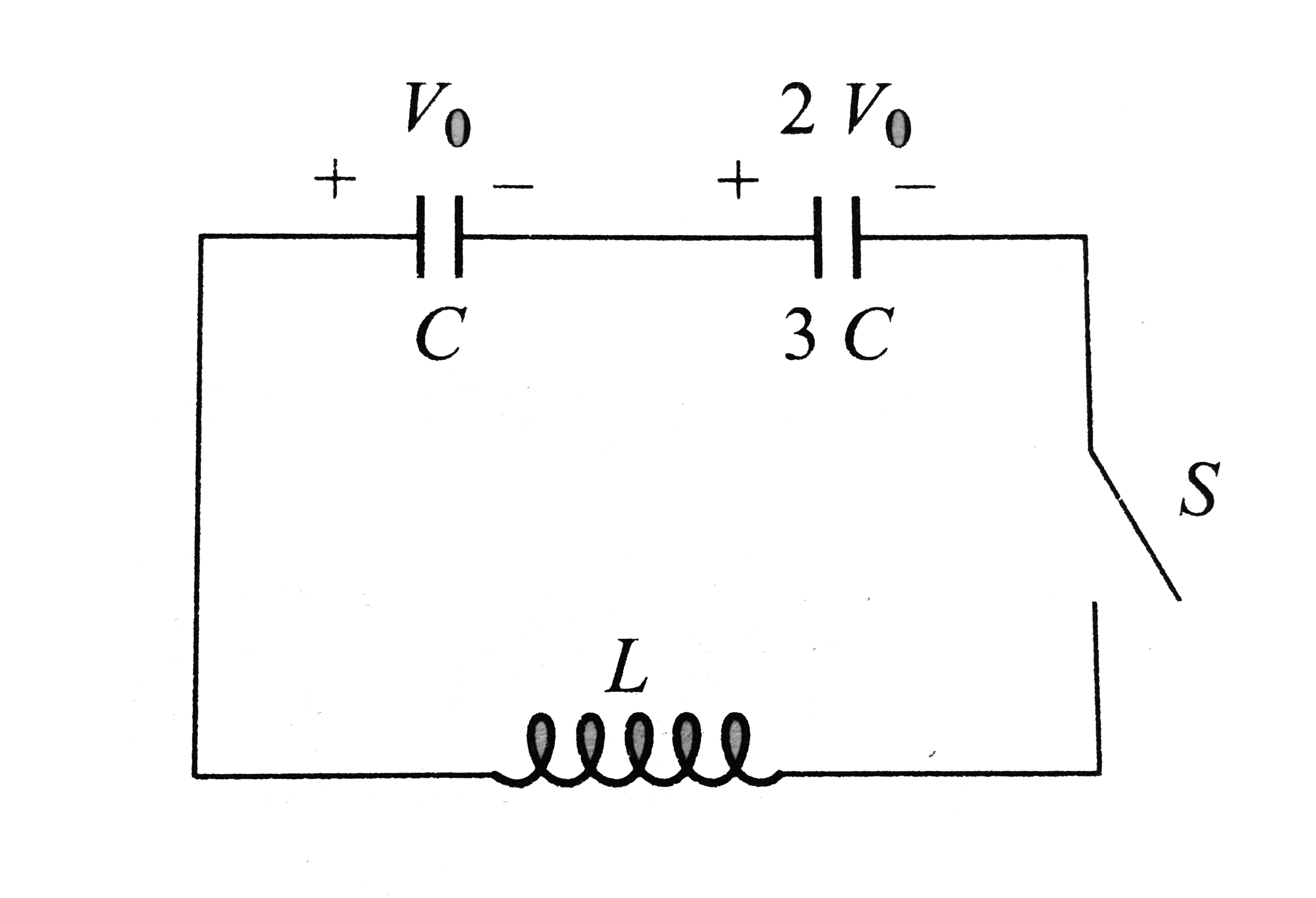
The maximum current in the inductor is
View SolutionIf n inductor of inductance L, radius r, current charges from 10 to I2. Find work done.
View Solution
Knowledge Check
A current of 1 A through a coil of inductance of 200 mH is increasing at a rate of 0.5As−1. The energy stored in the inductor per second is
A0.5Js−1B5.0Js−1C0.1Js−1D2.0Js−1In an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
A4sB3sC2sD1sIn an inductor of self-inductance L=2 mH, current changes with time according to relation i=t2e−t. At what time emf is zero ?
A4sB3sC2sD1s
A 10H inductor carries a current of 20A. How much ice at 0∘C could melted by the energy stored in the magnetic field of the inductor? Latent heat of ice is 22.6×10I3J/kg
View SolutionConsider the RL circuit in Fig. When the switch is closed in position 1 and opens in position 2, electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of PL/PR of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio PL/PR as a function of time.
c. If the time constant of circuit is t, what is the time at which PL=PR?
View SolutionA current of 2A is increasing at a rate of 4As−1 through a coil of inductance 1H. Find the energy stored in the inductor per unit time in the units of Js−1.
View SolutionObtain the expression for the magnetic energy stored in an ideal inductor of self inductance L when a current I passes through it.
Hence obtain the expression for the energy density of magentic field produced in the inductor.
View SolutionA 100mH coil carries a current of 1 ampere. Energy stored in its magnetic field is
View Solution
