In Boolena algebra equals
2
1
0
both 0 and 1
To solve the problem ¯¯¯1+¯¯¯1 in Boolean algebra, we can follow these steps:
1. Understand the Notation: In Boolean algebra, ¯¯¯1 represents the NOT operation applied to 1. The result of this operation is 0, since the NOT of 1 is 0.
2. Apply the NOT Operation: Calculate ¯¯¯1:
¯¯¯1=0
3. Substitute in the Expression: Now substitute ¯¯¯1 in the original expression:
¯¯¯1+¯¯¯1=0+0
4. Perform the Addition: In Boolean algebra, the addition operation corresponds to the OR operation. Therefore:
0+0=0
5. Conclusion: Thus, the final result of ¯¯¯1+¯¯¯1 is:
¯¯¯1+¯¯¯1=0
Final Answer:
The value of ¯¯¯1+¯¯¯1 in Boolean algebra is 0.
---
¯¯¯1=0
¯¯¯1+¯¯¯1=0+0
0+0=0
¯¯¯1+¯¯¯1=0
The value of ¯¯¯1+¯¯¯1 in Boolean algebra is 0.
Similar Questions
Knowledge Check
- Question 1 - Select One
In isosceles triangle ABC below , the measures of ∠BAC and ∠BCA are equal and ¯¯¯¯¯¯DE∣∣¯¯¯¯¯¯AC.The diagonals of trapeziod DECA intersect at F . The length of ¯¯¯¯¯¯DE is 9 centimeters , and the length of ¯¯¯¯¯¯AC is 27 centimeters . what is the length , in centimeters , of ¯¯¯¯¯¯FC ?
 A12B15C18D33
A12B15C18D33
Let ¯a,¯b,¯c be three non-coplanar vectors and ¯d be a non-zero vector, which is perpendicularto ¯a+¯b+¯c. Now, if ¯d=(sinx)(¯aׯb)+(cosy)(¯bׯc)+2(¯cׯa) then minimum value of x2+y2 is equal to
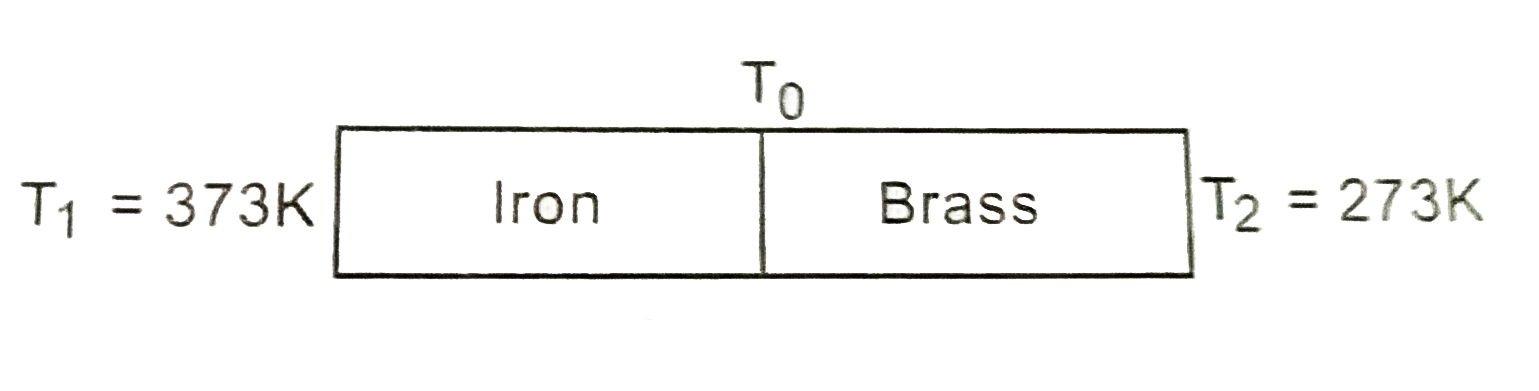
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .View Solution
.View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .View Solution
.View SolutionGiven four non zero vectors ¯a,¯b,¯cand¯d. The vectors ¯a,¯band¯c are coplanar but not collinear pair by pairand vector ¯d is not coplanar with vectors ¯a,¯band¯candˆ¯a¯b=ˆ¯b¯c=π3,(¯d¯b)=β ,If (¯d¯c)=cos−1(mcosβ+ncosα) then m−n is :
View SolutionLet →a be vector parallel to line of intersection of planes P1andP2 through origin. If P1is parallel to the vectors 2¯j+3¯kand4¯j−3¯k and P2 is parallel to ¯j−¯k and 3¯I+3¯j, then the angle between →a and 2¯i+¯j−2¯k is :
View Solutionlet ¯uand¯v be unit vectors. If ¯¯ω is a vector such that ¯¯ω+(¯¯ωׯu)=¯v. Then prove that the maximum volume of the parallelepiped formed by ¯u,¯vand¯¯ω is 1/2.
View SolutionABCD is parallelogram. If LandM are the middle points of BC and CD, then ¯¯¯¯¯¯AL+¯¯¯¯¯¯¯AM equals
View Solution

