ABCD is parallelogram. If LandM are the middle points of BC and CD, then ¯¯¯¯¯¯AL+¯¯¯¯¯¯¯AM equals
12→AC
23→AC
32→AC
34→AC
The correct Answer is:3
To solve the problem, we need to find the sum of the vectors ¯AL+¯AM in the context of the parallelogram ABCD where L and M are the midpoints of sides BC and CD respectively.
1. Define the Position Vectors:
Let the position vector of point A be →a, point B be →b, point C be →c, and point D be →d. Since ABCD is a parallelogram, we have:
→c=→a+→b(since →c=→a+→b)
→d=→b+→a(since →d=→b+→a)
2. Find the Midpoints L and M:
The position vector of midpoint L of BC is given by:
→L=→b+→c2=→b+(→a+→b)2=2→b+→a2=→b+→a2
The position vector of midpoint M of CD is given by:
→M=→c+→d2=(→a+→b)+(→b+→a)2=2→a+2→b2=→a+→b
3. Calculate Vectors ¯AL and ¯AM:
The vector ¯AL is:
¯AL=→L−→A=(→b+→a2)−→a=→b−→a2
The vector ¯AM is:
¯AM=→M−→A=(→a+→b)−→a=→b
4. Sum the Vectors:
Now, we add ¯AL and ¯AM:
¯AL+¯AM=(→b−→a2)+→b=2→b−→a2
5. Express in terms of →AC:
Since →AC=→c−→a=(→a+→b)−→a=→b, we can express the final result in terms of →AC:
¯AL+¯AM=32→AC
Final Result:
Thus, we conclude that:
¯AL+¯AM=32→AC
Let the position vector of point A be →a, point B be →b, point C be →c, and point D be →d. Since ABCD is a parallelogram, we have:
→c=→a+→b(since →c=→a+→b)
→d=→b+→a(since →d=→b+→a)
The position vector of midpoint L of BC is given by:
→L=→b+→c2=→b+(→a+→b)2=2→b+→a2=→b+→a2
The position vector of midpoint M of CD is given by:
→M=→c+→d2=(→a+→b)+(→b+→a)2=2→a+2→b2=→a+→b
The vector ¯AL is:
¯AL=→L−→A=(→b+→a2)−→a=→b−→a2
The vector ¯AM is:
¯AM=→M−→A=(→a+→b)−→a=→b
Now, we add ¯AL and ¯AM:
¯AL+¯AM=(→b−→a2)+→b=2→b−→a2
Since →AC=→c−→a=(→a+→b)−→a=→b, we can express the final result in terms of →AC:
¯AL+¯AM=32→AC
Thus, we conclude that:
¯AL+¯AM=32→AC
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - ASSIGNMENT (SECTION-B)
32 Videos
- VECTOR ALGEBRABOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - ASSIGNMENT (SECTION-C)
6 Videos
- VECTOR ALGEBRABOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - TRY YOURSELF
20 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
16 Videos
Similar Questions
Knowledge Check
In rectangle ABCD below ,¯¯¯¯¯¯BC is 16 inches long and ¯¯¯¯¯¯CD is 12 inches long . Points E,F and G are the midpoints of ¯¯¯¯¯¯AD,¯¯¯¯¯¯ABand¯¯¯¯¯¯BC respectively . What is the perimeter ,in inches , of pentagon CDEFG ?
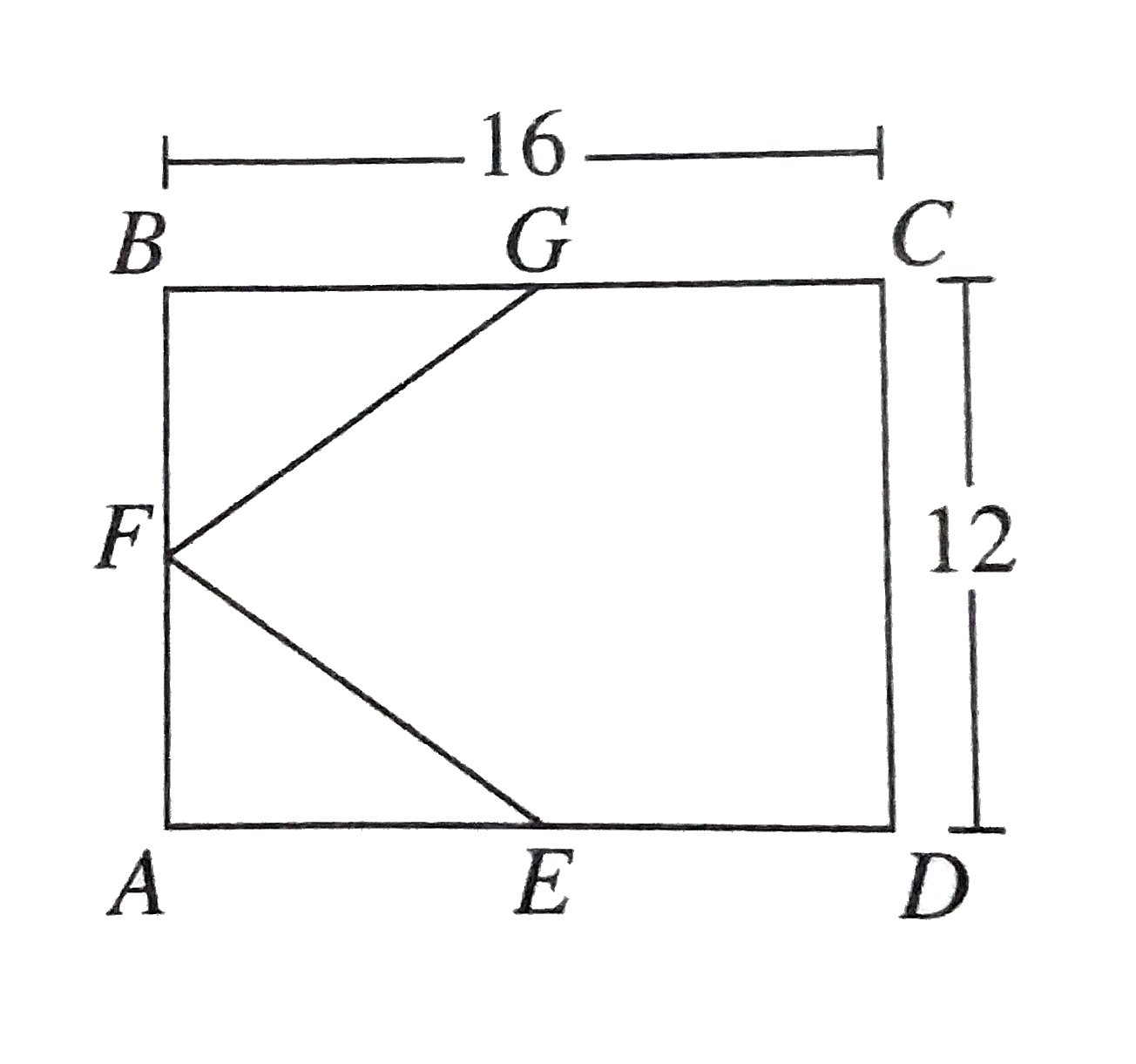 A48B56C96D144
A48B56C96D144
In the Boolean algebra ¯¯¯A.¯¯¯B equals
View SolutionGiven a parallelogram ABCD where X and Y are the mid-points of the sides BC and CD respectively . Prove that:
ar (ΔAXY)=38×ar(/gm)ABCD
View SolutionIf P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
View SolutionABCD is a parallelogram. E is the mid-point of AB and F is the mid-point of CD. GH is any line that intersects AD, EF and BC at G, P and H respectively. Prove that : GP=PH

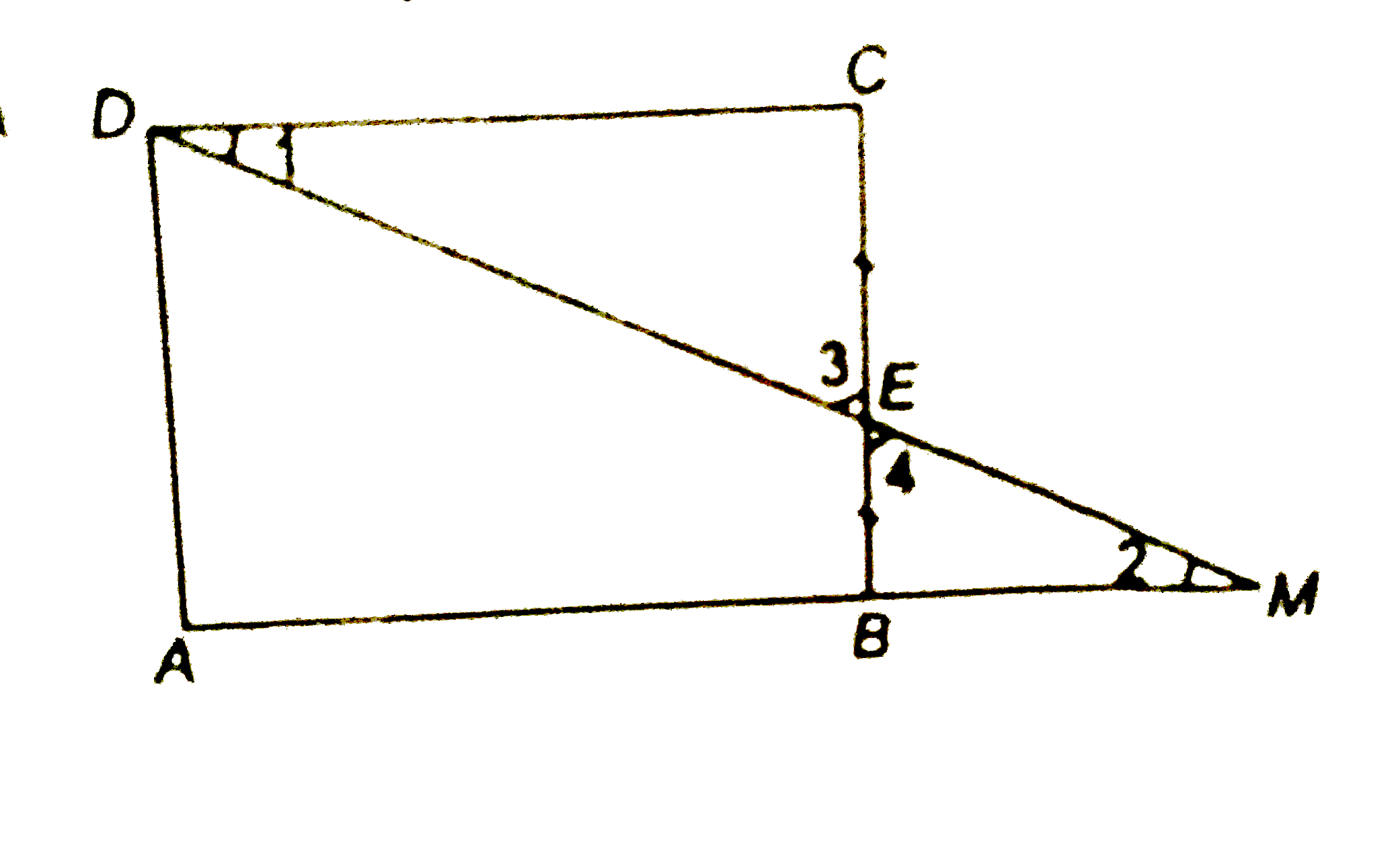
View SolutionIn the adjoining figure ABCD is a parallelogram, ABM is a line segment and E is the mid-point of BC. Prove that :
(i) ΔDCE≅ΔMBe (ii) AB=BM
(iii) AM=2DC
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

BC= BE
View SolutionIn the adjoining figure, ABCD is a quadrilateral. M and N are the points on AD and CD respectively such that AB=BC,∠ABM=∠CBN and ∠MBD=∠NBD. Prove that BM=BN.

View Solution
