A capacitor of capacitance 9nF having dielectric slab of εr=2.4 dielectric strength 20 MV/m and P.D.=20V calculate area of plates.
2.1×10−4m2
4.2×10−4m2
1.4×10−4m2
2.4×10−4m2
The correct Answer is:B
To solve the problem step by step, we will follow the given data and apply the relevant formulas.
Step 1: Identify the given values
- Capacitance, C=9nF=9×10−9F
- Dielectric constant, εr=2.4
- Dielectric strength, E=20MV/m=20×106V/m
- Potential difference, V=20V
Step 2: Calculate the distance between the plates (D)
The dielectric strength E is defined as the electric field strength, which can be expressed as:
E=VD
Rearranging this formula gives:
D=VE
Substituting the known values:
D=20V20×106V/m=2020×106=10−6m
Step 3: Use the capacitance formula for a capacitor with a dielectric
The capacitance C of a capacitor with a dielectric is given by:
C=ε0⋅A⋅εrD
Where:
- ε0 (the permittivity of free space) is approximately 8.85×10−12F/m
- A is the area of the plates
- D is the distance between the plates (calculated in Step 2)
Step 4: Rearranging the capacitance formula to find the area A
Rearranging the formula to solve for A:
A=C⋅Dε0⋅εr
Substituting the known values:
A=9×10−9F⋅10−6m8.85×10−12F/m⋅2.4
Step 5: Calculate the area A
Calculating the denominator:
8.85×10−12⋅2.4=2.124×10−11F/m
Now substituting back into the area formula:
A=9×10−9⋅10−62.124×10−11=9×10−152.124×10−11≈0.423×10−3m2
This can be expressed as:
A≈4.23×10−4m2
Final Answer
The area of the plates is approximately:
A≈4.23×10−4m2
- Capacitance, C=9nF=9×10−9F
- Dielectric constant, εr=2.4
- Dielectric strength, E=20MV/m=20×106V/m
- Potential difference, V=20V
The dielectric strength E is defined as the electric field strength, which can be expressed as:
E=VD
Rearranging this formula gives:
D=VE
Substituting the known values:
D=20V20×106V/m=2020×106=10−6m
The capacitance C of a capacitor with a dielectric is given by:
C=ε0⋅A⋅εrD
Where:
- ε0 (the permittivity of free space) is approximately 8.85×10−12F/m
- A is the area of the plates
- D is the distance between the plates (calculated in Step 2)
Rearranging the formula to solve for A:
A=C⋅Dε0⋅εr
Substituting the known values:
A=9×10−9F⋅10−6m8.85×10−12F/m⋅2.4
Calculating the denominator:
8.85×10−12⋅2.4=2.124×10−11F/m
Now substituting back into the area formula:
A=9×10−9⋅10−62.124×10−11=9×10−152.124×10−11≈0.423×10−3m2
This can be expressed as:
A≈4.23×10−4m2
The area of the plates is approximately:
A≈4.23×10−4m2
Similar Questions
A capacitor of capacitance 15 nF having dielectirc slab of εr=2.5 dielectric strength 30 MV/m and potential difference = 30 volt. Calculate the area of plate
View SolutionA capacitor of capacitance 2μF has a dielectric slab of dielectric constant 8 between its plates. The slab covers the entire volume between the plates. This capacitor is connected to a battery if EMF 20 V and fully charged Now with the battery still connected, the slab is removed from the capactor. during the removal, the work done by the battery is (in mJ).
View SolutionFind an expression for the capacitance of a parallel plate capacitor when a dielectric slab of dielectric constant K and thickness t=d2 but the same area on the plates is inserted between the the capacitors plate. (d=separation between the plates)
View SolutionA parallel plate capacitor of capacitance C (without dielectric) is filled by dielectric slabs as shown in figure. Then the new capacitance of the capacitor is

View SolutionAn isolated capacitor of capacitance C is charged to a potential V. Then a dielectric slab of dielectric constant K is inserted as shown. The net charge on four surfaces 1,2, 3 and 4 would be respectively.

View SolutionA parallel plate capacitor has a dielectric slab of dielectric constant K between its plates that covers 1/3 of the area of its plates, as shown in the figure. The total capacitance of the capacitor is C while that of the portion with dielectric in between is C1. When the capacitor is charged, the plate area covered by the dielectric gets charge Q1 and the rest of the area gets charge Q2. The electric field in the dielectric is E1 and that in the other portion is E2. Choose the correct option/options, ignoring edge effects.

View SolutionThe space between the plates of a parallel plate capacitor of capacitance C is filled with three dielectric slabs of identical size as shown in figure. If the dielectric constants of the three slabs are K1,K2andK3 find the new capacitance.

View SolutionA parallel plate capacitor is half filled with a dielectric slab of dielectric constant (K) and mass M. Capacitor is connected to a cell of e.m.f. E. Plates are held fixed on horizontal surface. A bullet of mass M hits the dielectric elastically and it is found that the dielectric slab just leaves out the capacitor. Find the speed of the bullet?
View SolutionThe dielectric to be used in a parallel-plate capacitor has a dielectric constant of 3.60 and a dielectric strength of 1.60×107V/m. The capacitor is to have a capacitance of 1.25×10−9F and must be able to withstand a maximum potential difference of 5500V. What is the minimum area the plates of the capacitor may have?
View SolutionFind the capacitance between A and B if two dielectric slabs (each of thickness d) of dielectric constants K1 and K2 and areas K1 and K2 and inserted between the plates of a parallel plate capacitor of plate area A.
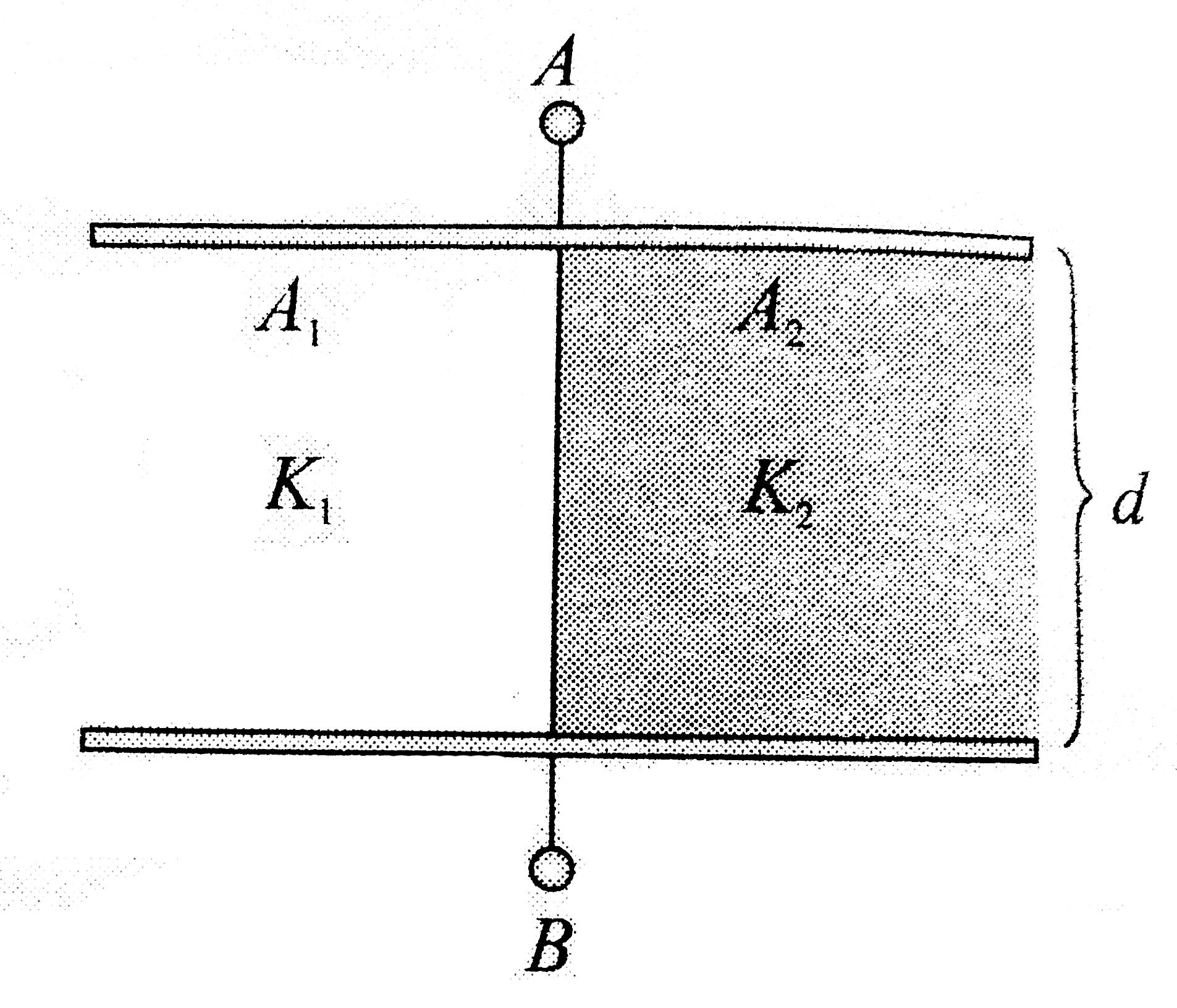 .
.
View Solution
