A capacitor of capacitance 15 nF having dielectirc slab of dielectric strength 30 MV/m and potential difference = 30 volt. Calculate the area of plate
The correct Answer is:A
To solve the problem step by step, we will follow the necessary formulas and calculations.
Step 1: Understand the given data
We have the following data:
- Capacitance (C) = 15 nF = 15×10−9 F
- Relative permittivity (ϵr) = 2.5
- Dielectric strength (E) = 30 MV/m = 30×106 V/m
- Potential difference (V) = 30 V
Step 2: Calculate the distance (d) using dielectric strength
The dielectric strength (E) is defined as the potential difference (V) divided by the distance (d):
E=Vd
Rearranging this gives:
d=VE
Substituting the values:
d=30V30×106V/m=3030×106=10−6m
Step 3: Use the formula for capacitance
The capacitance of a capacitor with a dielectric is given by:
C=ϵ0⋅ϵr⋅Ad
Where:
- ϵ0 (permittivity of free space) = 8.85×10−12F/m
- A is the area of the plates.
Step 4: Rearranging to find the area (A)
Rearranging the capacitance formula to solve for area A:
A=C⋅dϵ0⋅ϵr
Substituting the known values:
A=(15×10−9F)⋅(10−6m)(8.85×10−12F/m)⋅(2.5)
Step 5: Perform the calculation
Calculating the denominator:
ϵ0⋅ϵr=8.85×10−12⋅2.5=2.2125×10−11F/m
Now substituting back into the area formula:
A=(15×10−9)⋅(10−6)2.2125×10−11=15×10−152.2125×10−11=152.2125×10−4≈6.77×10−4m2
Final Result
The area of the plates A≈6.77×10−4m2.
We have the following data:
- Capacitance (C) = 15 nF = 15×10−9 F
- Relative permittivity (ϵr) = 2.5
- Dielectric strength (E) = 30 MV/m = 30×106 V/m
- Potential difference (V) = 30 V
The dielectric strength (E) is defined as the potential difference (V) divided by the distance (d):
E=Vd
Rearranging this gives:
d=VE
Substituting the values:
d=30V30×106V/m=3030×106=10−6m
The capacitance of a capacitor with a dielectric is given by:
C=ϵ0⋅ϵr⋅Ad
Where:
- ϵ0 (permittivity of free space) = 8.85×10−12F/m
- A is the area of the plates.
Rearranging the capacitance formula to solve for area A:
A=C⋅dϵ0⋅ϵr
Substituting the known values:
A=(15×10−9F)⋅(10−6m)(8.85×10−12F/m)⋅(2.5)
Calculating the denominator:
ϵ0⋅ϵr=8.85×10−12⋅2.5=2.2125×10−11F/m
Now substituting back into the area formula:
A=(15×10−9)⋅(10−6)2.2125×10−11=15×10−152.2125×10−11=152.2125×10−4≈6.77×10−4m2
The area of the plates A≈6.77×10−4m2.
Similar Questions
A capacitor of capacitance 9nF having dielectric slab of εr=2.4 dielectric strength 20 MV/m and P.D.=20V calculate area of plates.
View SolutionTwo parallel plate capacitors A and B have the same separation d=8.85×10−4m between the plates. The plate area of A and B are 0.04m2 and 0.02m2 respectively. A slab of dielectric constant (relative permittivity) K=9 has dimensions such that it can exactly fill the space between the plates of capacitor B.
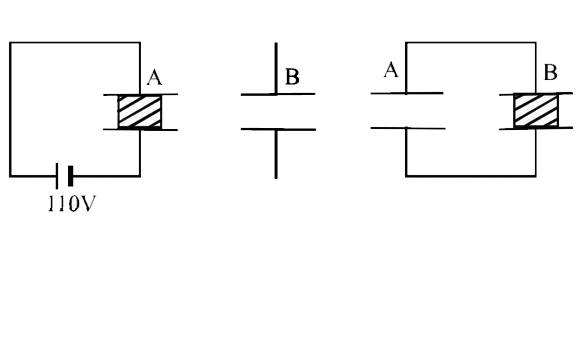
(i) The dielectric slab is placed inside. A as shown in figure (a). A is then charged to a potential difference of 110V. Calculate the capacitance of A and the energy stored in it.
The battery is disconnected and then the dielectric slab is moved from A. Find the work done by the external agency in removing the slab from A.
(iii) The same dielectric slab is now placed inside B, filling it completely, The two capacitors A and B are then connected as shown in figure(c). Calculate the energy stored in the system.
View SolutionThe capacitor of capacitance 4μF and 6μF are connected in series. A potential difference of 500 volts applied to the outer plates of the two capacitor system. Then the charge on each capacitor is numerically
View SolutionThe dielectric to be used in a parallel-plate capacitor has a dielectric constant of 3.60 and a dielectric strength of 1.60×107V/m. The capacitor is to have a capacitance of 1.25×10−9F and must be able to withstand a maximum potential difference of 5500V. What is the minimum area the plates of the capacitor may have?
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
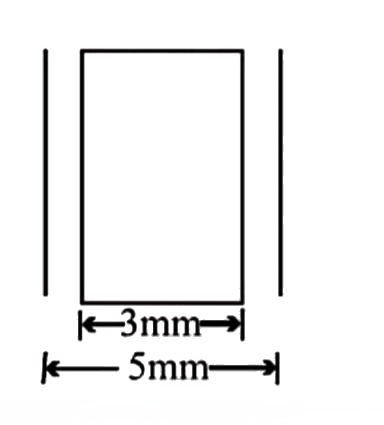
View SolutionAn air-cored capacitor of plate area A and separation d has a capacity C. Two dielectric slabs are inserted between its plates in two different manners as shown. Calculate the capacitance in each case.

View SolutionThe space between the plates of a parallel plate capacitor is completely filled with a material of resistivity 2×1011Ωm and dielectric constant 6. Capacity of the capacitor with the given dielectric medium between the plates is 20μF. Find the leakage current if a potential difference 2500V is applied across the capacitor.
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionA parallel plate capacitor of capacitance 100 microfarad is connected a power supply of 200 V. A dielectric slab of dielectric constant 5 is now inserted into the gap between the plates. (a) Find the extra charge flown through the power supply and the work done by the supply. (b) Find the change in the electrostatic energy of the electric field in the capacitor.
View SolutionA capacitor having a capacitance of 100μf is changed to a potential difference of 50V.(a) What is the magnitude of the charge on each plate? (b)The charging battery is disconnected and a dielectric of dielectric constant 2.5 is inserted . Calculate the new potential difference between the plate .(c) What charge would have produced this potential difference in absence of the dielectric slab.(d) Find the charge induced at a surface of the dielectric slab.
View Solution
