Find ratio of acceleration and angularr acceleration of com? If for the above diagram m=2kg and r=10 cm

a. $\frac{1}{5}$

b. $\frac{1}{10}$

c. $\frac{1}{15}$

d. $\frac{1}{20}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$a = \frac{F}{m} = \frac{20}{20} = 10$
$τ = I \propto$
$20 \times \frac{1}{10} = \frac{1}{z} \times 2 x {(0.1)}^{2} \times \propto$
$\propto = 200$
$∴ \frac{a}{\propto} = \frac{10}{200} = \frac{1}{20}$

Updated on:21/07/2023

Class 12 PHYSICS AIIMS 2019 25 MAY MORNING SHIFT

Similar Questions

Find acceleration $a$ and angular acceleration $α$ . If $F = 2 N, m = 1 k g$ and $l = 2 m$

View Solution
Find the acceleration of $3 k g$ mass when acceleration of 2kg mass is $m s^{- 2}$ as shwon in fig.

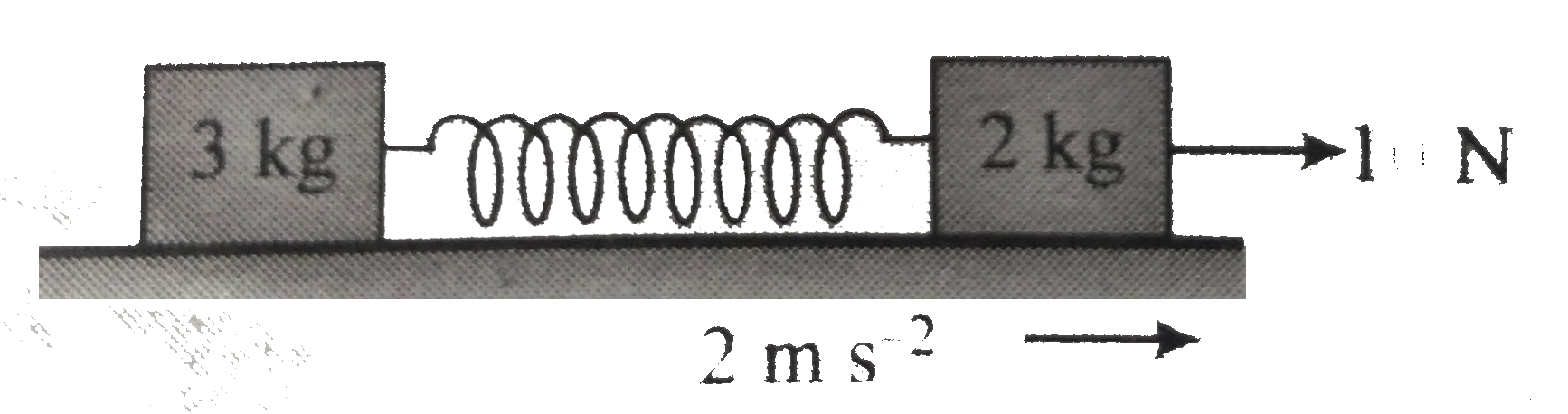
View Solution
For the system shown in figure, $M = 1 k g$ $m = 0.2$ kg, $r = 0.2 m$ calculate $(g = 10 m / s^{2})$
(a). The linear acceleration of hoop,
(b). The angular acceleration of the hoop of mass $M$ and
(c). The tension in the rope.
View Solution
Find the acceleration of 3 kg mass when acceleration of 2 kg mass is $2 m s^{- 2}$ as shown in figure-2.140

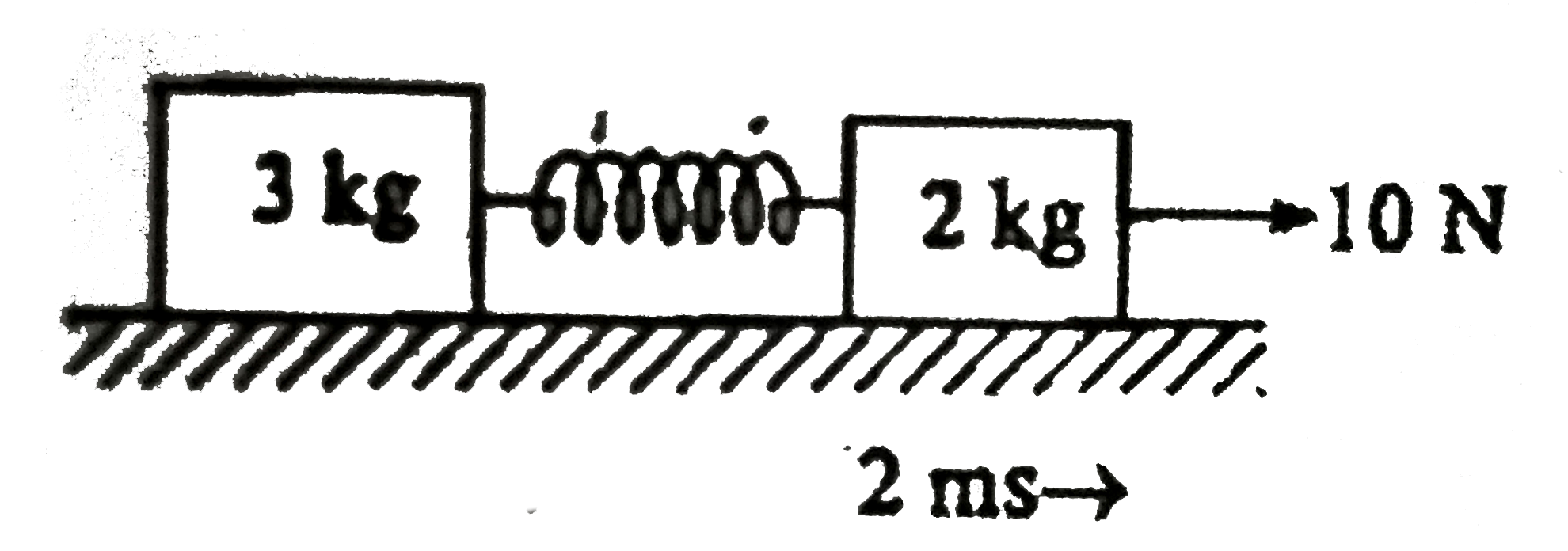
View Solution
A 2 kg block A is attached to one end of a light string that passes over an an ideal pulley and a 1 kg sleeve B slides down the other part of the string with an acceleration of $5 m / s^{2}$ with respect to the string. Find the acceleration of the block, acceleration of sleeve and tension in the steing. $[g = 10 m / s^{2}]$

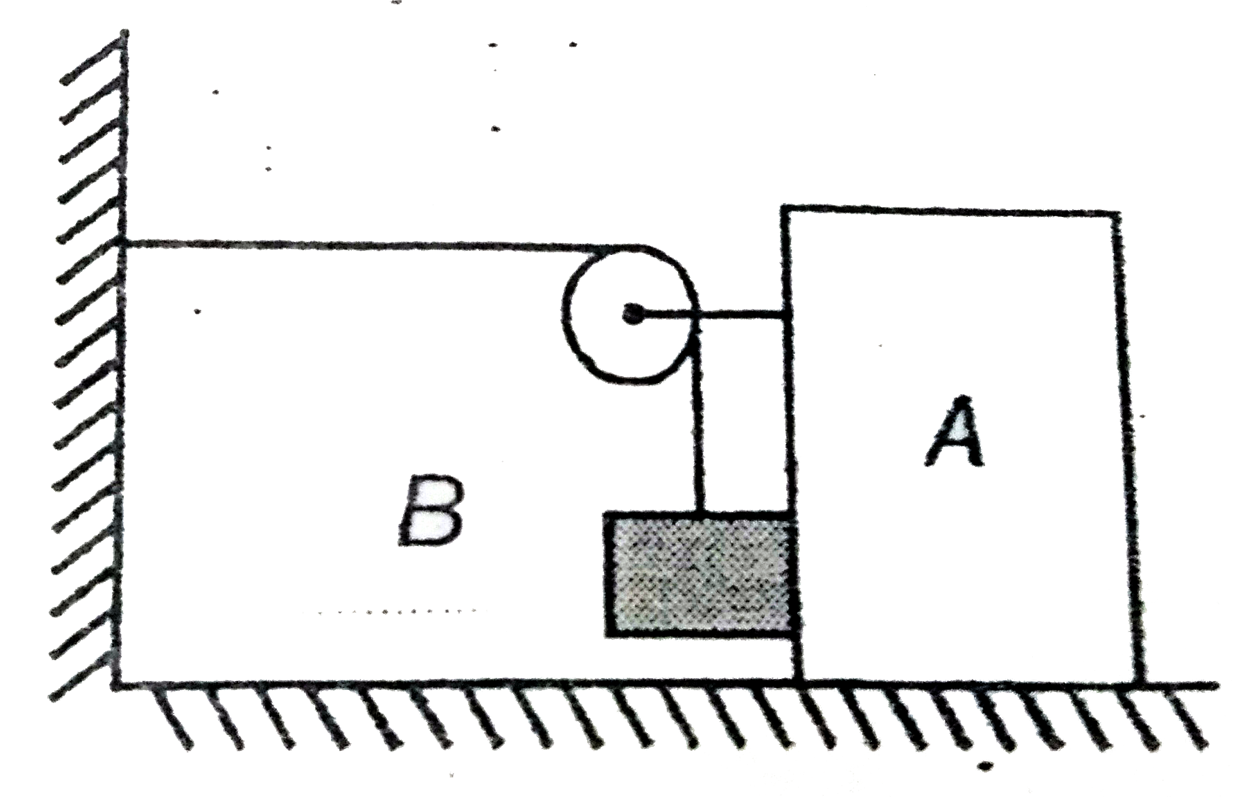
View Solution
Two masses are shown in above figure find acceleration of center of mass?
View Solution
A 5 kg block B is suspended from a cord attached to a 40 kg cart A . Find the accelerations of both the block and cart . ( All surfaces are frictionles ) ( g = $10 m / s^{2})$

View Solution
In figure shown if 2 kg block is moving at an acceleration $2 m / s^{2}$ , find the elongationin spring and acceleration of 4 kg block at this instant. Take g= $10 m / s^{2}$ .

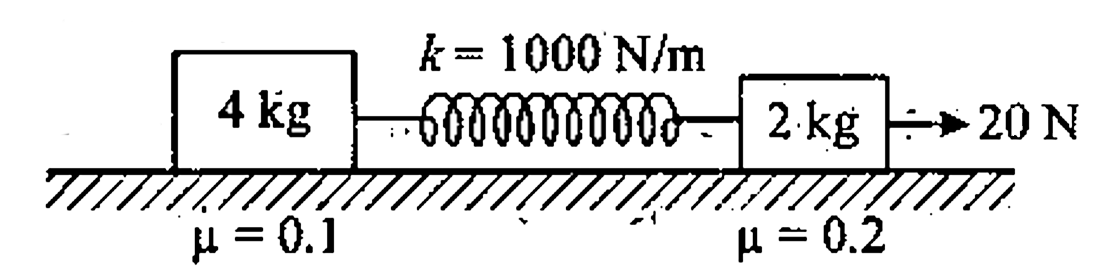
View Solution
Two particles of masses $2 k g$ and $4 k g$ are approaching towards each other with ccelerations $1 m / s^{2}$ and $2 m / s^{2}$ , respectively, on a smooth horizontal suface. Then find the acceleration of centre of mass of the system and direction of acceleration of CM.
View Solution
A block of mass $2 k g$ is kept on a truck moving with a constant acceleration. The height 'h' of the block is $60 c m$ and its width 'w' is $15 c m$ . The surface between the block and the truck is sufficiently rough toprevent slipping. The minimum acceleration of the truck at which the topple is (take $g = 10 m / s^{2}$ )

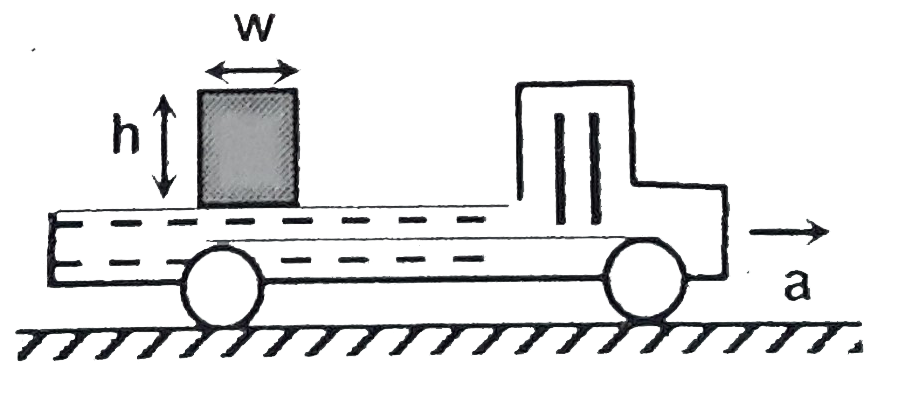
View Solution

Find ratio of acceleration and angularr acceleration of com? If for the above diagram m=2kg and r=10 cm

The correct Answer is:D

a=Fm=2020=10 τ=I∝ 20×110=1z×2x(0.1)2×∝ ∝=200 ∴a∝=10200=120

Similar Questions

Recommended Questions

$a = \frac{F}{m} = \frac{20}{20} = 10$
$τ = I \propto$
$20 \times \frac{1}{10} = \frac{1}{z} \times 2 x {(0.1)}^{2} \times \propto$
$\propto = 200$
$∴ \frac{a}{\propto} = \frac{10}{200} = \frac{1}{20}$