
For the system shown in figure, M=1kg m=0.2 kg, r=0.2m calculate (g=10m/s2)
(a). The linear acceleration of hoop,
(b). The angular acceleration of the hoop of mass M and
(c). The tension in the rope.

If α be the angular acceleration of the hoop and a be the acceleration if its centre, accelaration of m would be αr+a
Here Tr=Iα [where I= moment of inertia of the hoop about the horizontal axis passing through its centre].
Also, T=Ma and mg−T=m[a+ar]
solving we get
a=mg[M=2m]=21.4=1.43m/s2
Hence, T=1.43N
and α=TrI=TMr=7.15rad/s2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Find acceleration a and angular acceleration α. If F=2N,m=1kg and l=2m

View SolutionIf acceleration of A is 2m/s2 to left and acceleration of B is 1m/s2 to left, then acceleration of C is-
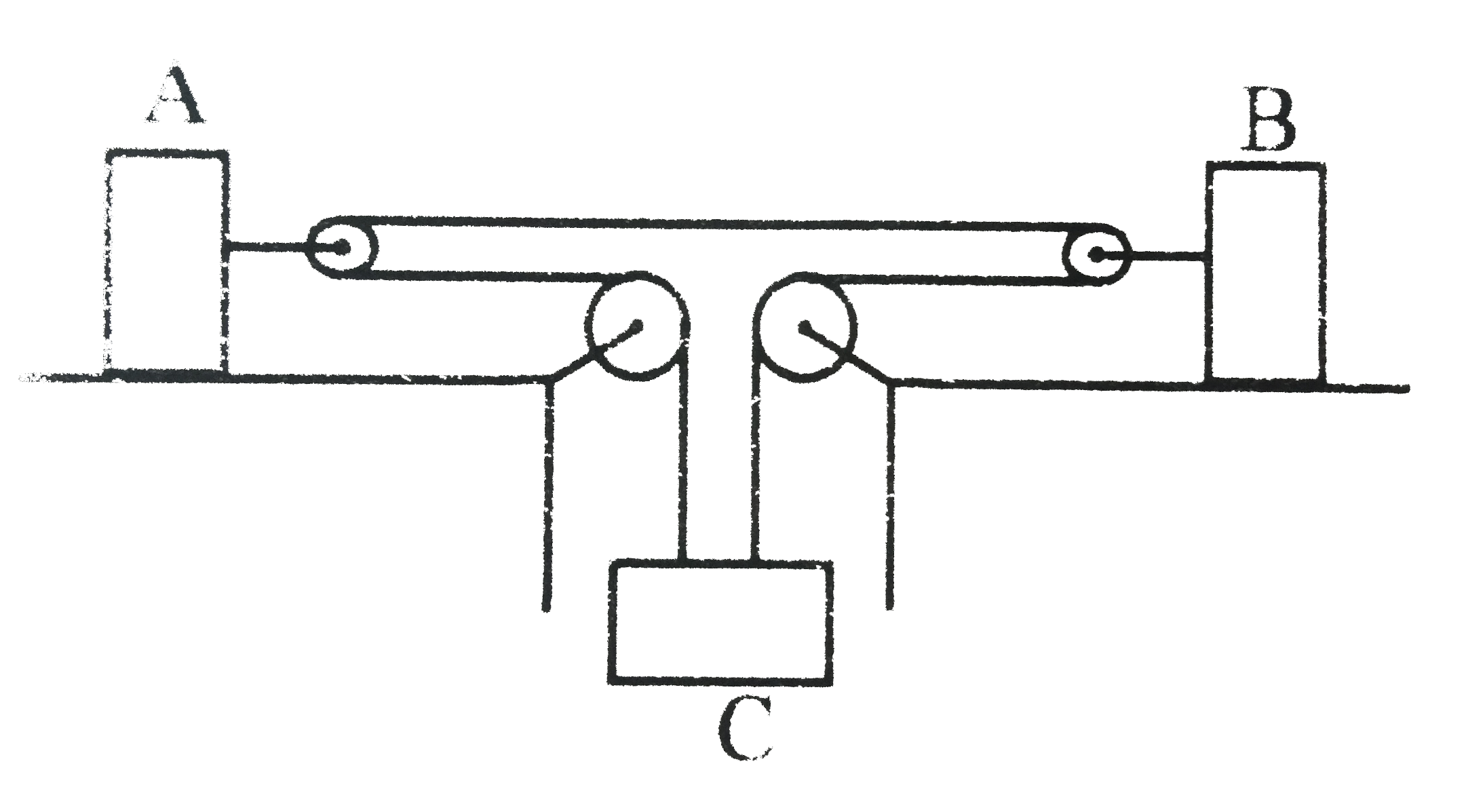
View SolutionIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
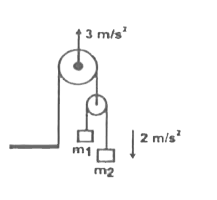
View SolutionConsider the system shown in figure
Mass of block A= 3m ,
Mass of block B= 2m .
Find the acceleration of A and B.

View SolutionIf the system shown in the figure is rotated in a horizontal circle with angular velocity ω . Find (g=10m/s2)
(a) the minimum value of ω to start relative motion between the two blocks.
(b) tension in the string connecting m1 and m2 when slipping just starts between the blocks
The coefficient of frition between the two masses is 0.5 and there is no friction between m2 and ground. The dimensions of the masses can be neglected. (Take R=0.5m,m1=2Kg,m2=1Kg)

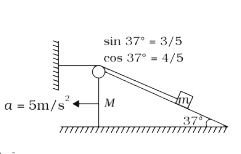
View SolutionAs shown in the figure, if acceleration of M with respect to ground is 5m/s2, then :
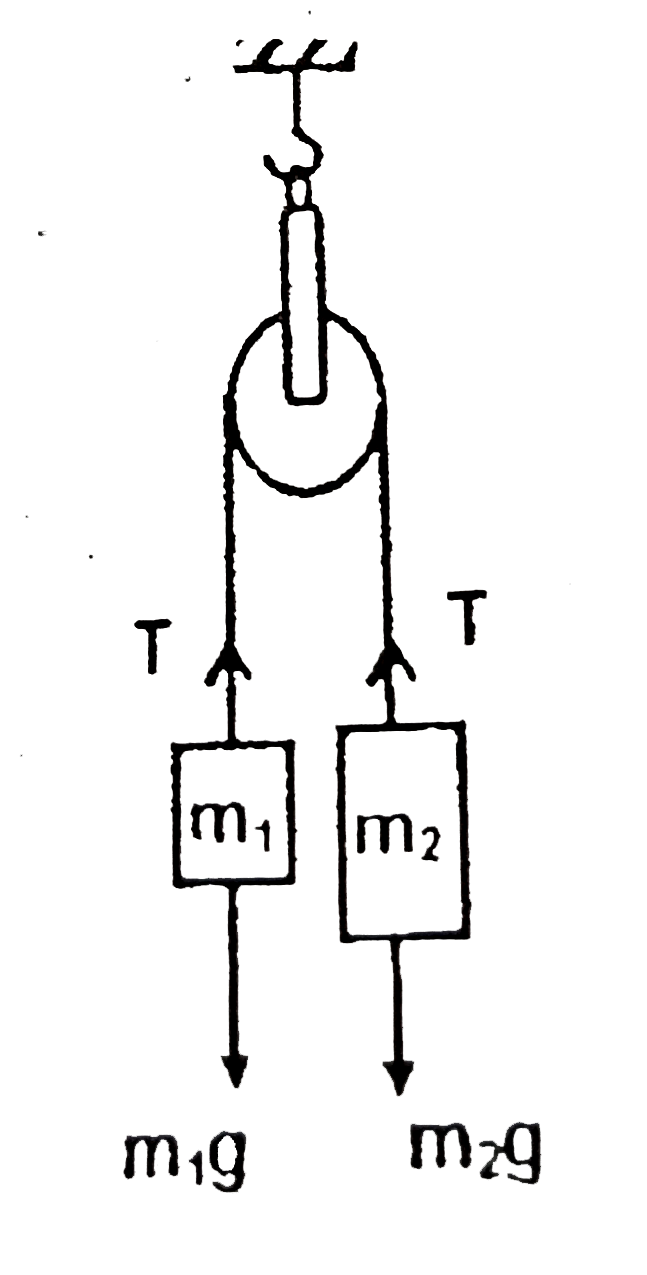
View SolutionConsider the case of two bodies of masses m1 and m2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations :
(i) when m1>m2. In this case
a=(m1−m2m1+m2)g and T=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)g and T=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0, T=mg
If m1=10kg, m2=6kg and g=10m/s2
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string
View SolutionIn the figure shown ,find :(g=10m/s2)

(a) acceleration of 1kg,2kg and 3kg blocks and
(b) tension T1 and T2.
View SolutionTwo blocks shown in figure are connected by a heavy uniform rope of mass 4kg. An upward force of 200N is applied as shown
(a) What is the acceleration of the system .
(b)What is the tension at the top of the rope ?
( c) What is the tension at the mid- point of the rop
(Takeg=9.8m/s2)

View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:

View Solution
