Ratio of electric and magnetic field due to moving point charge if its speed is 4.5×105m/s
2×1011
3×1011
2×108
3×1012
The correct Answer is:A
To solve the problem of finding the ratio of the electric field (E) to the magnetic field (B) due to a moving point charge, we can follow these steps:
Step 1: Write the formulas for electric and magnetic fields
The electric field (E) due to a point charge q at a distance r is given by:
E=kqr2
where k is Coulomb's constant, k=14πϵ0.
The magnetic field (B) due to a moving charge is given by:
B=μ04π⋅qvr2
where v is the velocity of the charge and μ0 is the permeability of free space.
Step 2: Set up the ratio EB
Now, we need to find the ratio EB:
EB=kqr2μ04π⋅qvr2
Step 3: Simplify the ratio
In the ratio, r2 and q will cancel out:
EB=kμ04π⋅v
This can be rewritten as:
EB=4πkμ0v
Step 4: Substitute k and simplify further
Substituting k=14πϵ0:
EB=4π⋅14πϵ0μ0v=1ϵ0μ0v
Step 5: Use the relationship between ϵ0, μ0, and the speed of light
We know that:
c2=1ϵ0μ0
Thus, we can substitute:
EB=c2v
Step 6: Substitute the values
Given v=4.5×105m/s and c=3×108m/s:
c2=(3×108)2=9×1016
Now substituting into the ratio:
EB=9×10164.5×105
Step 7: Calculate the final value
Now, we can perform the division:
EB=94.5×1016−5=2×1011
Final Answer
Thus, the ratio of the electric field to the magnetic field due to the moving point charge is:
EB=2×1011
The electric field (E) due to a point charge q at a distance r is given by:
E=kqr2
where k is Coulomb's constant, k=14πϵ0.
B=μ04π⋅qvr2
where v is the velocity of the charge and μ0 is the permeability of free space.
Now, we need to find the ratio EB:
EB=kqr2μ04π⋅qvr2
In the ratio, r2 and q will cancel out:
EB=kμ04π⋅v
This can be rewritten as:
EB=4πkμ0v
Substituting k=14πϵ0:
EB=4π⋅14πϵ0μ0v=1ϵ0μ0v
We know that:
c2=1ϵ0μ0
Thus, we can substitute:
EB=c2v
Given v=4.5×105m/s and c=3×108m/s:
c2=(3×108)2=9×1016
Now substituting into the ratio:
EB=9×10164.5×105
Now, we can perform the division:
EB=94.5×1016−5=2×1011
Thus, the ratio of the electric field to the magnetic field due to the moving point charge is:
EB=2×1011
Similar Questions
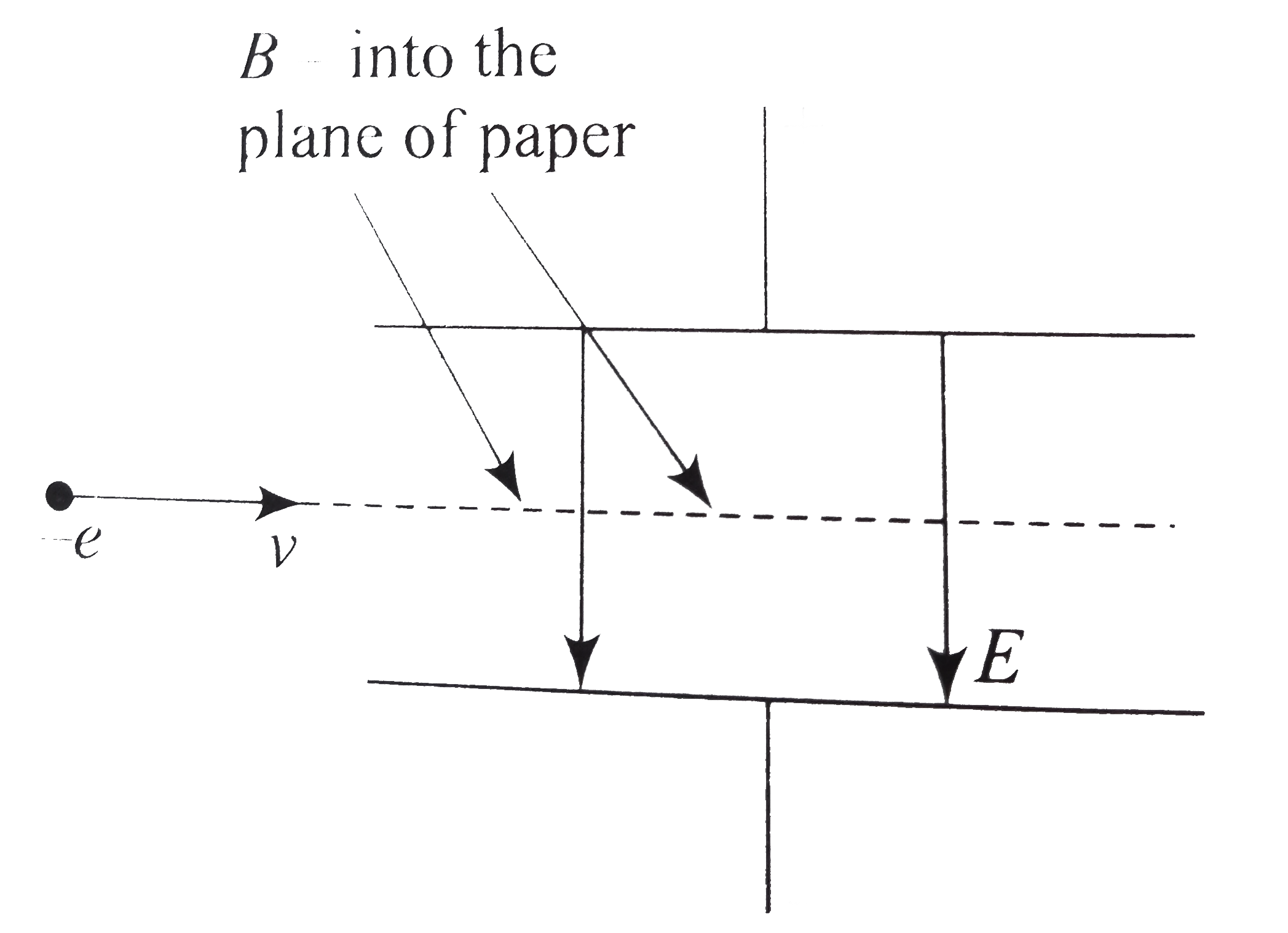
Electrons taveling at a velocity of 2.4×106ms−1 enter a region of crossed electric and magnetic fields as shoen in Fig. If the electric field is 3.0×106 Vm and the flux density of the magnetic field is 1.5 T, the electrons upon entering the region of the crossed fields will
View SolutionA uniformly charged ring of radius R is rotated about its axis with constant linear speed v of each of its particle. The ratio of electric field to magnetic field at a point P on the axis of the ring distant x=R from centre of ring is (c is speed of light )

View Solution
Knowledge Check
At a given place on earth's surface the horizontal component of earths magnetic field is 2×10−5T and resultant magnetic field is 4×10−5T. The angles of dip at this place is
A30∘B60∘C90∘D44∘
A velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
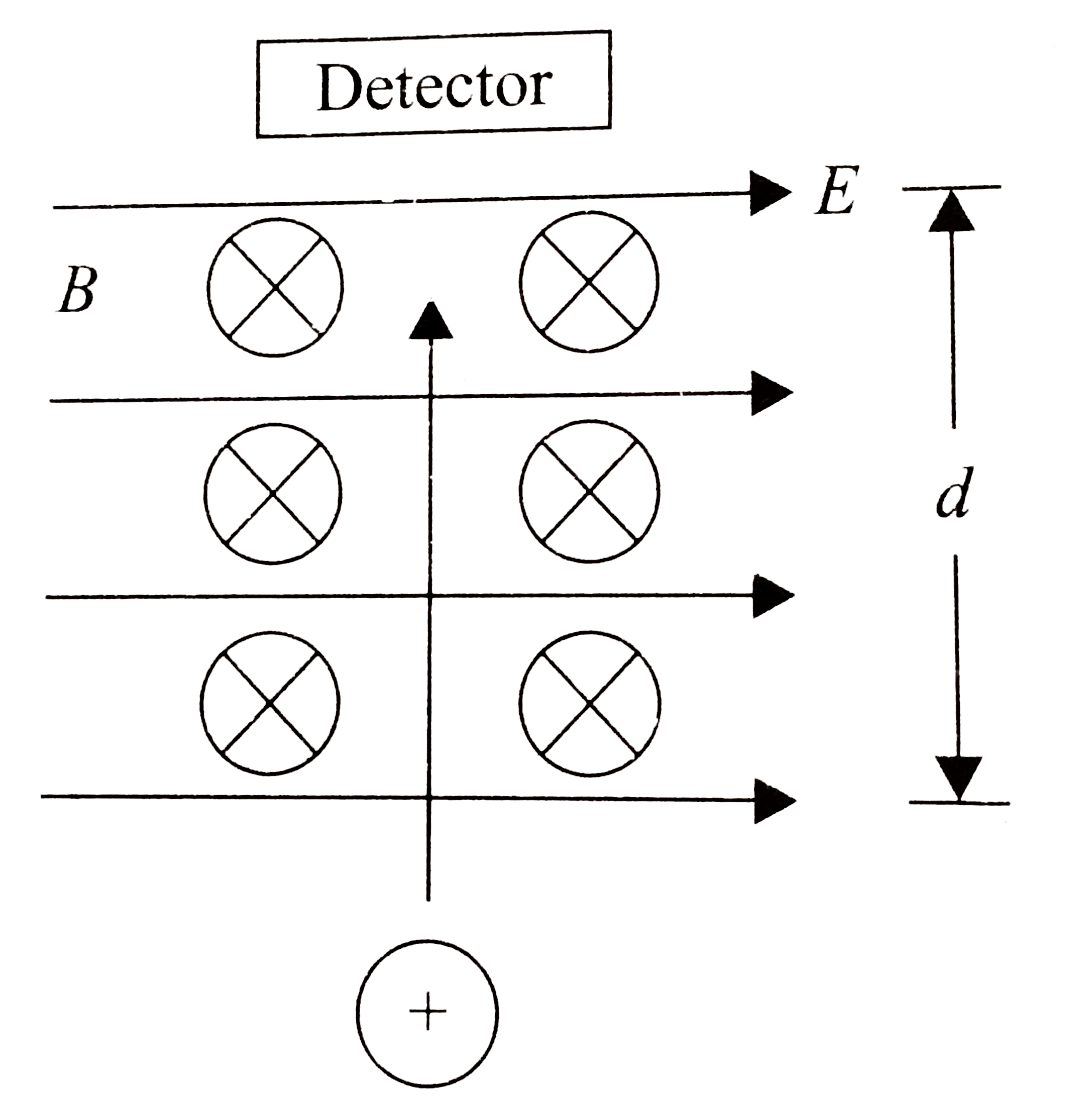
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?
View SolutionIn a certain region of space a uniform and constant electric field and a magnetic field parallel to each other are present. A proton is fired from a point A in the field with speed V=4×104m/s at an angle of α with the field direction. The proton reaches a point B in the field where its velocity makes an angle β with the field direction. If sinαsinβ=√3. Find the electric potential difference between the points A and B. Take mp (mass of proton) =1.6×10−27kg and e (magnitude of electronic charge) =1.6×10−19C.
View SolutionA charged particle with a velocity 2×103ms−1 passes undeflected through electric field and magnetic fields in mutually perpendicular directions. The magnetic field is 1.5 T. the magnitude of electric field will be
View SolutionA proton of mass 1.67×10−27 kg and charge 1.6×10−19C is shot a uniform magnetic field, and perpendicular to the field with a velocity 5×106m/s. If the magnetic induction of the field is 1 tesla, find
(i) The radius of the circular path
View SolutionA conductor of 3m in length is moving perpendicularly to magnetic field of 10−4 tesla with the speed of 102m/s, then the e.m.f. produced across the ends of conductor will be
View SolutionA point charge is moving in a circular path of radius 10cm with angular frequency 40π ra//s. The magnetic field produced by it at the center is 3.8×10−10T. Then the value of charge is:
View SolutionA point charge is moving in a circular path of radius 10cm with angular frequency 40π ra//s. The magnetic field produced by it at the center is 3.8×10−10T. Then the value of charge is:
View Solution
