A 8,000 kg engine pulls a train of 5 wagons, each of 2,000 kg along a horizontal track. If the engine exerts a force of 40,000 N and track offers a force of friction of 5,000 N, then calculate the : net accelerating force.
To solve the problem, we need to calculate the net accelerating force acting on the train system. Here are the steps to find the solution:
1. Identify the Forces Involved:
- The engine exerts a force (F_engine) of 40,000 N in the forward direction.
- The frictional force (F_friction) opposing the motion is 5,000 N.
2. Calculate the Net Force:
- The net force (F_net) can be calculated using the formula:
Fnet=Fengine−Ffriction
- Substituting the values:
Fnet=40,000N−5,000N
3. Perform the Calculation:
- Calculate the net force:
Fnet=40,000N−5,000N=35,000N
4. Conclusion:
- The net accelerating force acting on the train system is 35,000 N.
Final Answer:
The net accelerating force is 35,000 N.
- The engine exerts a force (F_engine) of 40,000 N in the forward direction.
- The frictional force (F_friction) opposing the motion is 5,000 N.
- The net force (F_net) can be calculated using the formula:
Fnet=Fengine−Ffriction
- Substituting the values:
Fnet=40,000N−5,000N
- Calculate the net force:
Fnet=40,000N−5,000N=35,000N
- The net accelerating force acting on the train system is 35,000 N.
The net accelerating force is 35,000 N.
Topper's Solved these Questions
Similar Questions
A 8,000 kg engine pulls a train of 5 wagons, each of 2,000 kg along a horizontal track. If the engine exerts a force of 40,000 N and track offers a force of friction of 5,000 N, then calculate the :acceleration of the train.
View SolutionA 8000kg engine pulls a train of 5wagons, each of 2000kg, along a horizontal track. If the engine exerts a force of 40000N and the track offers a frictional force of 5000N, then calculate:
(a) the net accelerating force, (b) the acceleration of the train, and
(c ) the force of wagon 1 on wagon 2.
View Solution
Knowledge Check
A 8000kg engine pulls a train of 5wagons, each of 2000kg, along a horizontal track. If the engine exerts a force of 40000N and the track offers a frictional force of 5000N, then calculate:
(a) the net accelerating force, (b) the acceleration of the train, and
(c ) the force of wagon 1 on wagon 2.A50000 N, 2.0 m/s2, 15000 NB35000 N, 1.94 m/s^2, 15520 NC50000 N, 2.5 m/s^2, 9000 NDNONETwo ropes are puling a large ship at rest of mass 1×106kg into harbour. Rope A exerts a force of 40,000N and rope B exerts a force of 30,000N.
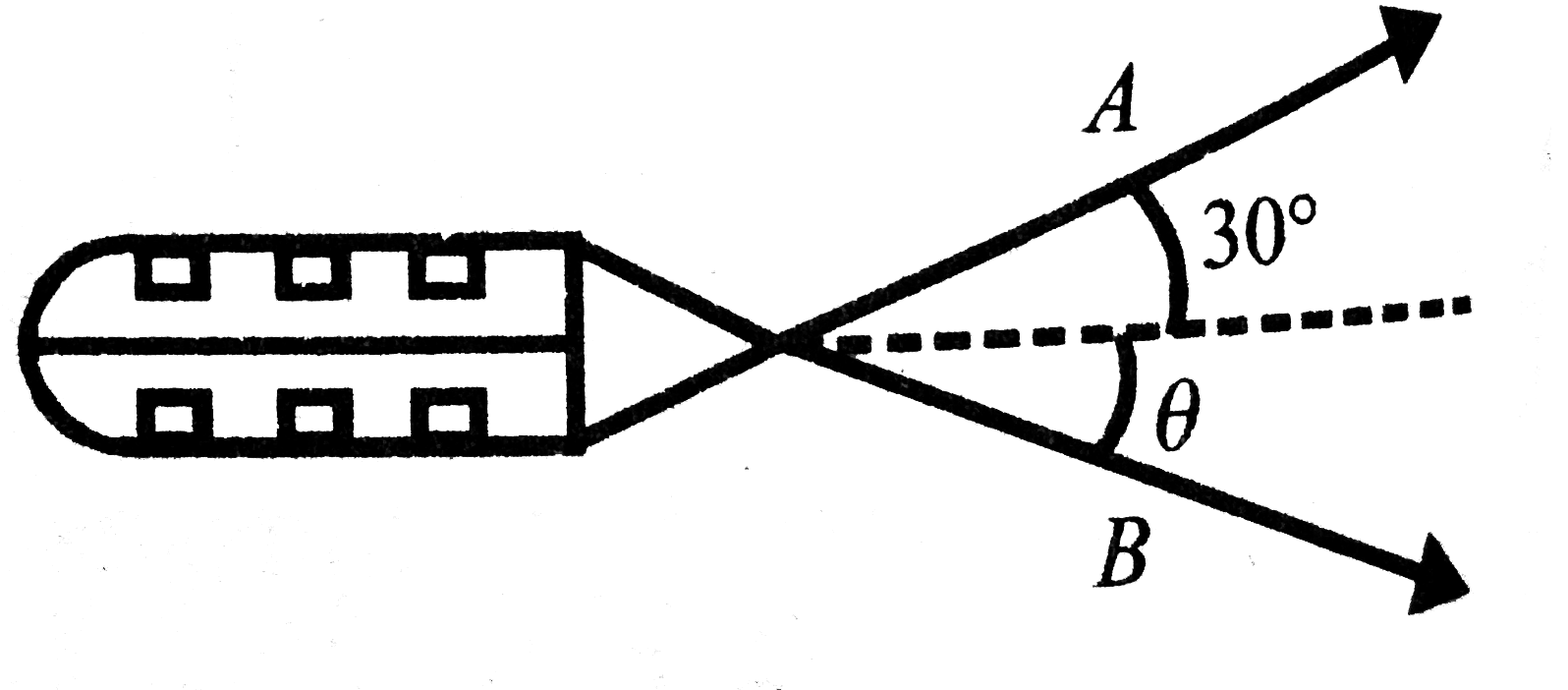
The angle θ if the slip is to move directly forward isAsin−1(49)Bsin−1(23)Csin−1(√32)Dnone of theseTwo ropes are puling a large ship at rest of mass 1×106kg into harbour. Rope A exerts a force of 40,000N and rope B exerts a force of 30,000N.
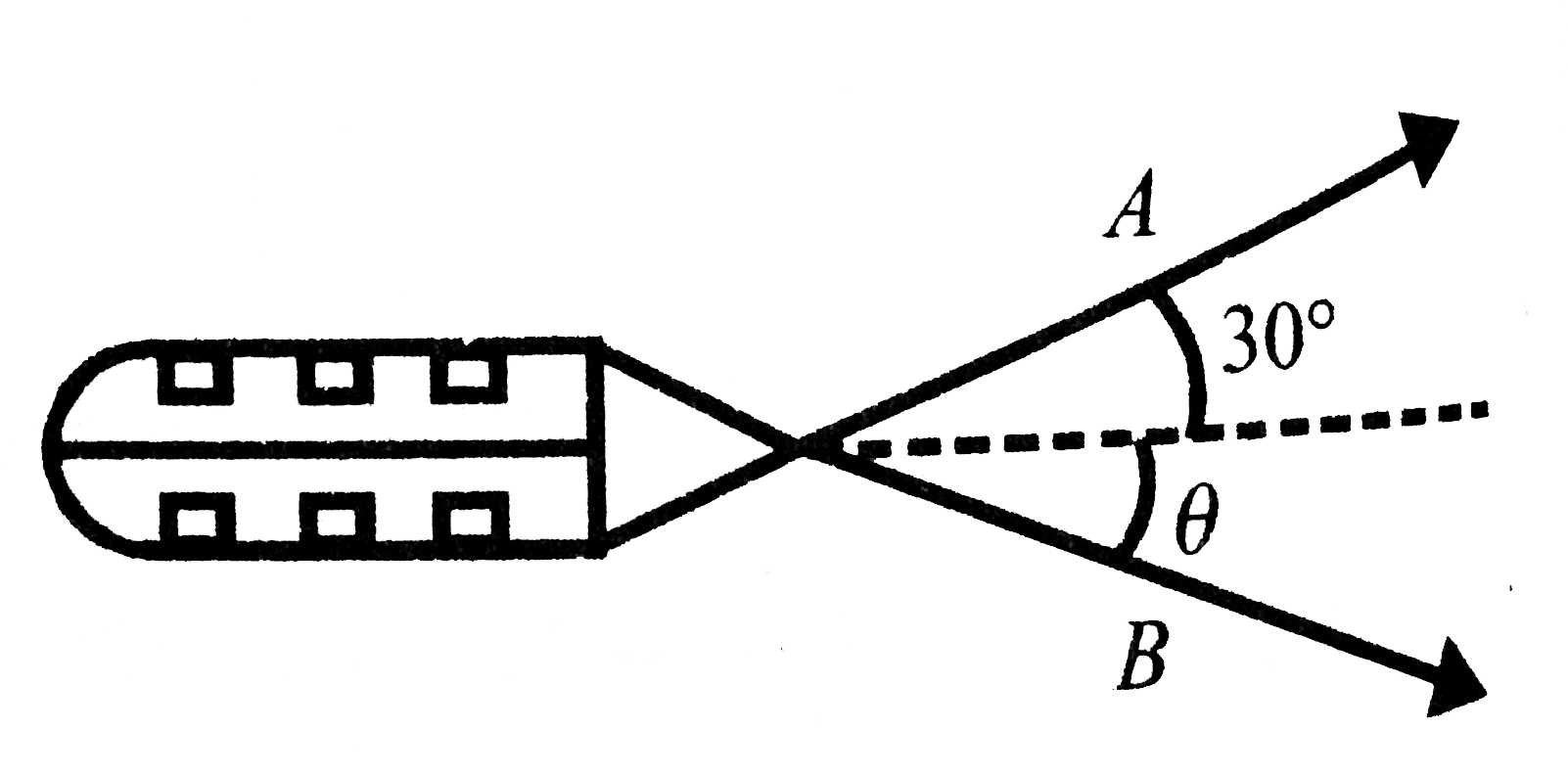
The time for the ship to travel 6m to the the dock isA1min30sB1minC40sD20s
A 8000kg engine pulls a train of 5wagons, each of 2000kg, along a horizontal track. If the engine exerts a force of 40000N and the track offers a frictional force of 5000N, then calculate:
(a) the net accelerating force, (b) the acceleration of the train, and
(c ) the force of wagon 1 on wagon 2.
View SolutionA 1000 kg engine pulls a train of 4 wagons each of 2500 kg along a horizontal railway track . If the engine exerts a force of 50000 N on wagons and track offers force of friction 10000 N, then calculate
(i) The net accelerating force
(ii) The acceleration of the train
(iii) The force of wagon -1 on wagon - 2
View SolutionA 1000 kg engine pulls a train of 4 wagons each of 2500 kg along a horizontal railway track . If the engine exerts a force of 50000 N on wagons and track offers force of friction 10000 N, then calculate
(i) The net accelerating force
(ii) The acceleration of the train
(iii) The force of wagon -1 on wagon - 2
View SolutionA 8000kg engine pulls a train of 5wagons, each of 2000kg, along a horizontal track. If the engine exerts a force of 40000N and the track offers a frictional force of 5000N, then calculate:
(a) the net accelerating force, (b) the acceleration of the train, and
(c ) the force of wagon 1 on wagon 2.
View SolutionWhat force is required to exert a pressure of 40,000 Pa on an area of 1 cm2 ?
View Solution
