Find the equivalent resistance when the following are connected in parallel: 1Ω and 100Ω
To find the equivalent resistance when resistors are connected in parallel, we can use the formula:
1Req=1R1+1R2
Where:
- Req is the equivalent resistance,
- R1 is the resistance of the first resistor,
- R2 is the resistance of the second resistor.
1. Identify the resistances:
- Given R1=1Ω
- Given R2=100Ω
2. Apply the formula for parallel resistances:
1Req=1R1+1R2
Substituting the values:
1Req=11+1100
3. Calculate the individual fractions:
1Req=1+0.01=1.01
4. Find the equivalent resistance:
To find Req, take the reciprocal of 1.01:
Req=11.01≈0.9901Ω
5. Final Result:
The equivalent resistance when 1 Ω and 100 Ω are connected in parallel is approximately:
Req≈0.99Ω
- Req is the equivalent resistance,
- R1 is the resistance of the first resistor,
- R2 is the resistance of the second resistor.
- Given R1=1Ω
- Given R2=100Ω
1Req=1R1+1R2
Substituting the values:
1Req=11+1100
1Req=1+0.01=1.01
To find Req, take the reciprocal of 1.01:
Req=11.01≈0.9901Ω
The equivalent resistance when 1 Ω and 100 Ω are connected in parallel is approximately:
Req≈0.99Ω
Topper's Solved these Questions
Similar Questions
Knowledge Check
The values of two resistors are (5.2±0.2) kΩ and (10.0±0.1) kΩ. What is the percentage error in the equivalent resistance when they are connected in parallel?
A0.02B0.05C0.07D0.1
Judge the equivalent resistance when the following are connected in parallel:
1ω and 106ω .
View SolutionJudge the equivalent resistance when the following are connected in parallel.
(a) 1Ωand106Ω
(b) 1Ωand108Ωand106Ω.
View SolutionJudge the equivalent resistance when the following are connected in parallel (i) 1Ω and 106Ω, (ii) 1Ω and 103Ω and 106Ω
View SolutionWhen resistors 1 and 2 are connected in series, the equivalent resistance is 20.0Ω. When they are connected in parallel, the equivalent resistance is 3.75Ω. What are (a) the smaller resistance and (b) the larger resistance of these two resistors?
View SolutionCalculate the resistance of two coils if their equivalent resistance in series and parallel are respectively 18Ω and 4Ω
View SolutionThree resistances of 2Ω,3Ωand6Ω are first connected in series and the equivalent resistance is found to be……… Then the three resistances are connected in parallel Now its equivalent resistance is………
View SolutionFind equivalent emf of four different cells which are connected in parallel. Their emf's and internal resistance are 1 volt, 1Ω,2 volt, 1Ω,3 volt, 1Ω,4 volt, 2Ω and their connection is given below .
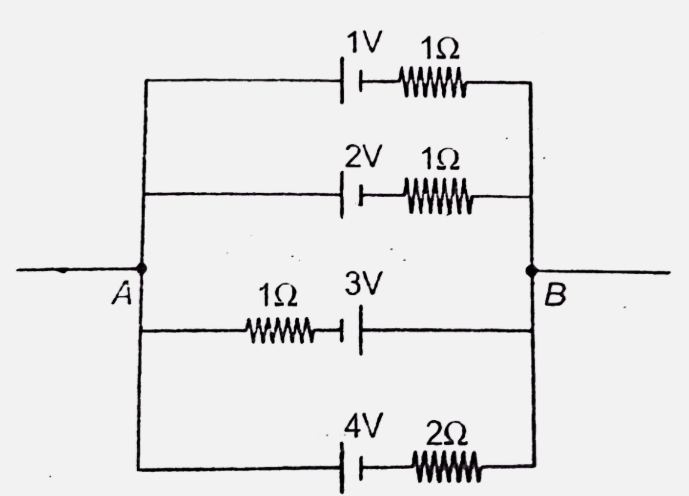
View Solution
