A quantitative relationship between the temperature and rate constant is given by :
Nernst equation
Arrhenius equation
van't Hoff equation
Henderson equation
The correct Answer is:B
To derive the quantitative relationship between temperature and the rate constant, we can follow these steps:
Step 1: Understand the Arrhenius Equation
The Arrhenius equation describes how the rate constant (k) of a chemical reaction depends on temperature (T) and activation energy (Ea). The equation is given by:
k=Ae−EaRT
where:
- k = rate constant
- A = Arrhenius factor (frequency factor)
- Ea = activation energy
- R = universal gas constant (8.314 J/(mol·K))
- T = temperature in Kelvin
Step 2: Analyze the Components
In the Arrhenius equation:
- The term e−EaRT represents the fraction of molecules that have enough energy to overcome the activation energy barrier.
- As temperature (T) increases, the value of EaRT decreases, leading to an increase in the exponential term, and thus an increase in the rate constant k.
Step 3: Implications of the Equation
From the Arrhenius equation, we can conclude that:
- The rate constant k increases with an increase in temperature.
- The relationship is exponential, meaning small increases in temperature can lead to significant increases in the rate constant.
Step 4: Conclusion
The quantitative relationship between temperature and the rate constant is encapsulated in the Arrhenius equation. This equation allows chemists to predict how changes in temperature will affect the speed of a reaction.
Summary
The Arrhenius equation provides a quantitative relationship between temperature and the rate constant of a reaction, showing that as temperature increases, the rate constant also increases due to the exponential factor related to activation energy.
---
The Arrhenius equation describes how the rate constant (k) of a chemical reaction depends on temperature (T) and activation energy (Ea). The equation is given by:
- k = rate constant
- A = Arrhenius factor (frequency factor)
- Ea = activation energy
- R = universal gas constant (8.314 J/(mol·K))
- T = temperature in Kelvin
In the Arrhenius equation:
- The term e−EaRT represents the fraction of molecules that have enough energy to overcome the activation energy barrier.
- As temperature (T) increases, the value of EaRT decreases, leading to an increase in the exponential term, and thus an increase in the rate constant k.
From the Arrhenius equation, we can conclude that:
- The rate constant k increases with an increase in temperature.
- The relationship is exponential, meaning small increases in temperature can lead to significant increases in the rate constant.
The quantitative relationship between temperature and the rate constant is encapsulated in the Arrhenius equation. This equation allows chemists to predict how changes in temperature will affect the speed of a reaction.
The Arrhenius equation provides a quantitative relationship between temperature and the rate constant of a reaction, showing that as temperature increases, the rate constant also increases due to the exponential factor related to activation energy.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CHEMICAL KINETICSEXERCISE - ISC EXAMINATION QUESTIONS (PART-I (OBJECTIVE QUESTIONS ) C .CORRECT THE FOLLOWING STATEMENTS )12videos
CHEMICAL KINETICS
- BOOK - ICSECHAPTER - CHEMICAL KINETICSEXERCISE - ISC EXAMINATION QUESTIONS (PART-I (OBJECTIVE QUESTIONS ) D. MATCH THE FOLLOWING )3videos
CHEMICAL KINETICS
- BOOK - ICSECHAPTER - CHEMICAL KINETICSEXERCISE - ISC EXAMINATION QUESTIONS (PART-I (OBJECTIVE QUESTIONS ) A.FILL IN THE BLANKS)12videos
CHEMICAL KINETICS
- BOOK - ICSECHAPTER - BIOMOLECULESEXERCISE - ISC EXAMINATION QUSTIONS (PART-I)(DESCRIPTIVE QUESTIONS)21videos
BIOMOLECULES
- BOOK - ICSECHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - EXERCISE (PART - II (DESCRIPTIVE QUESTIONS) (LONG ANSWER QUESTIONS))19videos
CHEMISTRY IN EVERYDAY LIFE
Similar Questions
Knowledge Check
- Question 1 - Select One
Volume : Temperature relationship is given by
ABoyleBGay LussacCDaltonDCharles
The relationship between α and β is given by
View SolutionThe effect of temperature on the rate constant of a reaction is given by
View SolutionWhich of the following shows correct relation between volume and temperature at constant pressure for a given amount of gas
View SolutionGive the mathematical relationship between the extent of adsorption and pressure at constant temperature and explain the symbols used.
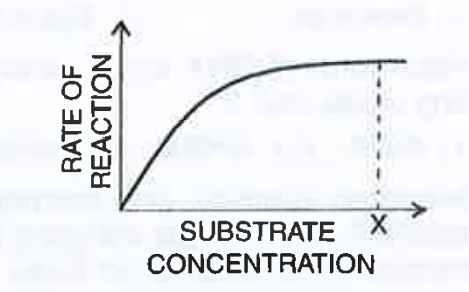
View SolutionThe given graph is showing the relationship between the rate of enzyme reaction and concentration of substrate. At concentration of substrate greater than X, the
 View Solution
View SolutionWhat is the effect of temperature on the rate constant of reaction? How can this temperature effect on the rate constant be represented quantitatively?
View SolutionDistinguish between 'rate expression' and 'rate constant' of a reaction.
View Solution