Write the following steps in sequential order to verify the laws of reflection.
(A) Draw a normal at the point where the two lines PQ and P, Q, meet. (B) Remove the pins and the mirror and join P, Q similarly join P.Q. (C) View the image of P and Q and fix two more pins P, and Q, such that the images of pins P, Q and P, Q are along the same line. (D) Draw a straight line on a white paper spread on the table and fix a plane mirror on the line. (E) Fix two pins P and Q in front of the mirror. (F) Measure the angle of incidence and angle of reflection and compare them to verify the law reflection
DABECF
ACDBFE
DECBAF
DBACEF
The correct Answer is:C
Topper's Solved these Questions
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - TEST YOUR CONCEPTS (VERY SHORT ANSWER TYPE QUESTIONS (MATCH THE COLUMN))
3 Videos
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - TEST YOUR CONCEPTS (VERY SHORT ANSWER TYPE QUESTIONS (ANSWER THE QUESTIONS))
20 Videos
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - TEST YOUR CONCEPTS (VERY SHORT ANSWER TYPE QUESTIONS (FILL IN THE BLANKS))
9 Videos
- KINEMATICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - KINEMATICSEXERCISE - ASSESSMENT TEST (TEST 2 (SELECT THE CORRECT ALTERNATIVE)
15 Videos
- MACHINES AND TOOLSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MACHINES AND TOOLSEXERCISE - CONCEPT APPLICATION (LEVEL 2)
12 Videos
Similar Questions
The points P (4, 1) and Q (-2, 4) are reflected in line y = 3. Find the co-ordinates of P', the image of P and Q', the image of Q.
View SolutionPoints P and Q trisect the line segment joining the points A(-2, 0) and B(0,8) such that, P is near to A. Find the coordinates of points P and Q.
View Solution
Knowledge Check
Write the following steps in sequential order to verify the laws of reflection.
(A) Draw a normal at the point where the two lines PQ and P1Q1 meet.
(B) Remove the pins and the mirror and join P,Q similarly join P1,Q1.
(C) View the image of P and Q and fix two more pins P1andQ1 such that the images of pins P,Q and P1,Q1 are along the same line.
(D) Draw a straight line on a white paper spred on the table and fix a plane mirror on the line.
(E) Fix two pins P and Q in front of mirror.
(F) Measure the angle of incidence and angle of reflection and copare them to verify the law reflection.ADABECFBACDBFECDECBAFDDBACEFArrange the following steps in sequential order to verify laws of reflection of light.
(A) Place a mirror on MM' and looking at the pins P and Q from the other side of the normal, observe their images.
(B) Fix a white paper to a drawing board and draw a straight line MM' and a line ON perpendicular to MM' on the paper.
(C) Fix two more pins P' and Q' in line with the images of the pins P and Q.
(D) Draw a line PO such that it makes suitable acute angle with the normal and fix two pins P and Q on the line, which is the incident ray.
(E) Measure ∠PON, the angle of incidence and ∠(P'ON), the angle of reflection.
(F) Remove the plane mirror and join P' and O. OP' is the reflected ray.
(G) Repeat the experiment for different angles of incidence and tabulate the results.AB A E C D F GBB D A C F E GCB A D C E F GDB D C E F A GIf p and q are two statements , then (p→q)⇒(~p→~p) is
AContradictionBTautologyCNeither (i) nor (ii)DNone of these
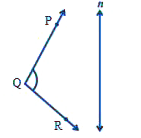
Draw the images P' , Q' and R' of the point P, Q and R respectively in the line n (Fig . 9. 18). Join P' Q' and Q' R' to form an angle P' Q' R' Measure ∠PQRand∠P'Q'R' . Are the two angles equal ?
View SolutionThe line segment joining the points (3, −4) and (1, 2) is trisected at the points P and Q . If the coordinates of P and Q are (p, −2) and (5/3, q) respectively. Find the values of p and q .
View SolutionPoints P and Q trisect the line segment joining the points A (-2,0) a and B(0,8) such that ,P is near to A . Find the coordinates of points P and Q.
View SolutionPoints P and Q trisect the line segment joining the points A(-2, 0) and B(0, 8) such that, P is near to A. Find the coordinates of points P and Q.
View SolutionThe image of P(a,b) on the line y=−x is Q and the image of Q on the line y=x is 'R' find the mid-point of 'P' and 'R'
View Solution
