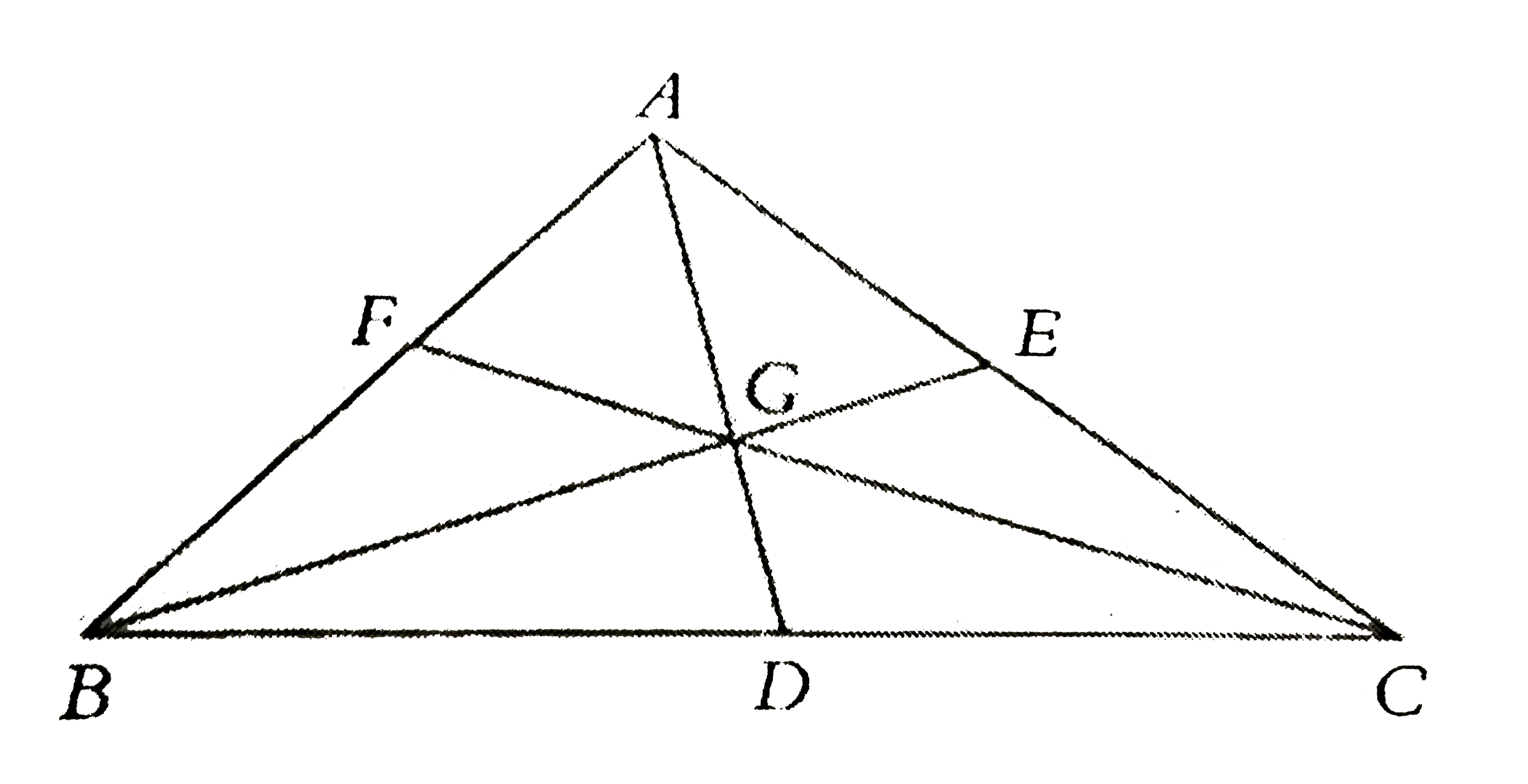
In the above are the medians. G is the centroid. What is the ratio of the areas of ?
The correct Answer is:
Step by step video, text & image solution for In the above DeltaABC, bar(AD),bar(BE) , and bar(CF) are the medians. G is the centroid. What is the ratio of the areas of DeltaBGD and DeltaGCE? by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - very Short answer Type Question
25 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Short answer Type Question
29 Videos
- FORMULASBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)
8 Videos
- INDICES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -2
12 Videos
Similar Questions
Knowledge Check
In ΔABC, the medians AD and BE meet at G. The ratio of the areas of ΔBDG and the quadrilateral GDCE is :
A1:2B1:3C2:3D3:4If G is the centroid of Δ ABC, then ¯¯¯¯¯¯CA+¯¯¯¯¯¯CB =
A3 ¯¯¯¯¯¯GCB3 ¯¯¯¯¯¯CGC3 ¯¯¯¯¯¯ABD3 ¯¯¯¯¯¯GAIn a ΔABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of ΔABC=72cm2
A12B16C24D8
In ΔABC,∣∣¯¯¯¯¯¯CB∣∣=a,∣∣¯¯¯¯¯¯CA∣∣=band∣∣¯¯¯¯¯¯AB∣∣=c.CD is the median through the vertex C. Then ¯¯¯¯¯¯CA.¯¯¯¯¯¯CD=
View SolutionLet O be an interior point of ΔABC such that ¯¯¯¯¯¯OA+2¯¯¯¯¯¯OB+3¯¯¯¯¯¯OC=0. Then the ratio of a ΔABC to area of ΔAOC is
View SolutionIn △ABC, the medians AD. BE and CF meet at O. What is the ratio of the area of △ABD to the area of △AOE ?
View SolutionIn △ABC , the medians AD, BE and CF meet at O. What is the ratio of the area of △ABD to the area of △AOE ?
View Solution
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.
View Solution