
In the above figure , DF is parallel to MN . EGH is an isosceles triangle , where EG=EHand∠GEH=50∘. If EM and EN are the bisectors of the ∠DEGand∠FEH , then
(i) Show that ∠DEM=∠FEN.
(ii) Show that ∠GEM=∠HEN.
Step by step video & image solution for In the above figure , DF is parallel to MN . EGH is an isosceles triangle , where EG=EHandangleGEH=50^(@). If EM and EN are the bisectors of the angleDEGandangleFEH , then (i) Show that angleDEM=angleFEN. (ii) Show that angleGEM=angleHEN. by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - TEST YOUR CONCEPTS (ESSAY TYPE QUESTIONS)
5 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - CONCEPT APPLICATION (Level 1)
60 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - TEST YOUR CONCEPTS ( VERY SHORT ANSWER TYPE QUESTIONS)
28 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
In an isosceles triangle ABC, with AB=AC, the bisectors of B and C intersect each other at O. Join A to O. Show that :
(i) OB=OC
(ii) AO bisects A
View SolutionThe figure above shows the race track in which ABCD is a square of side 21 km and MQR is an isosceles triangle. One can travel along the square at the speed of 5 kmph, along the circle at the speed of 4 kmph and along the triangle at 3 kmph. While travelling along these tracks one has to change tracks, at a point where two or three intersect each other.
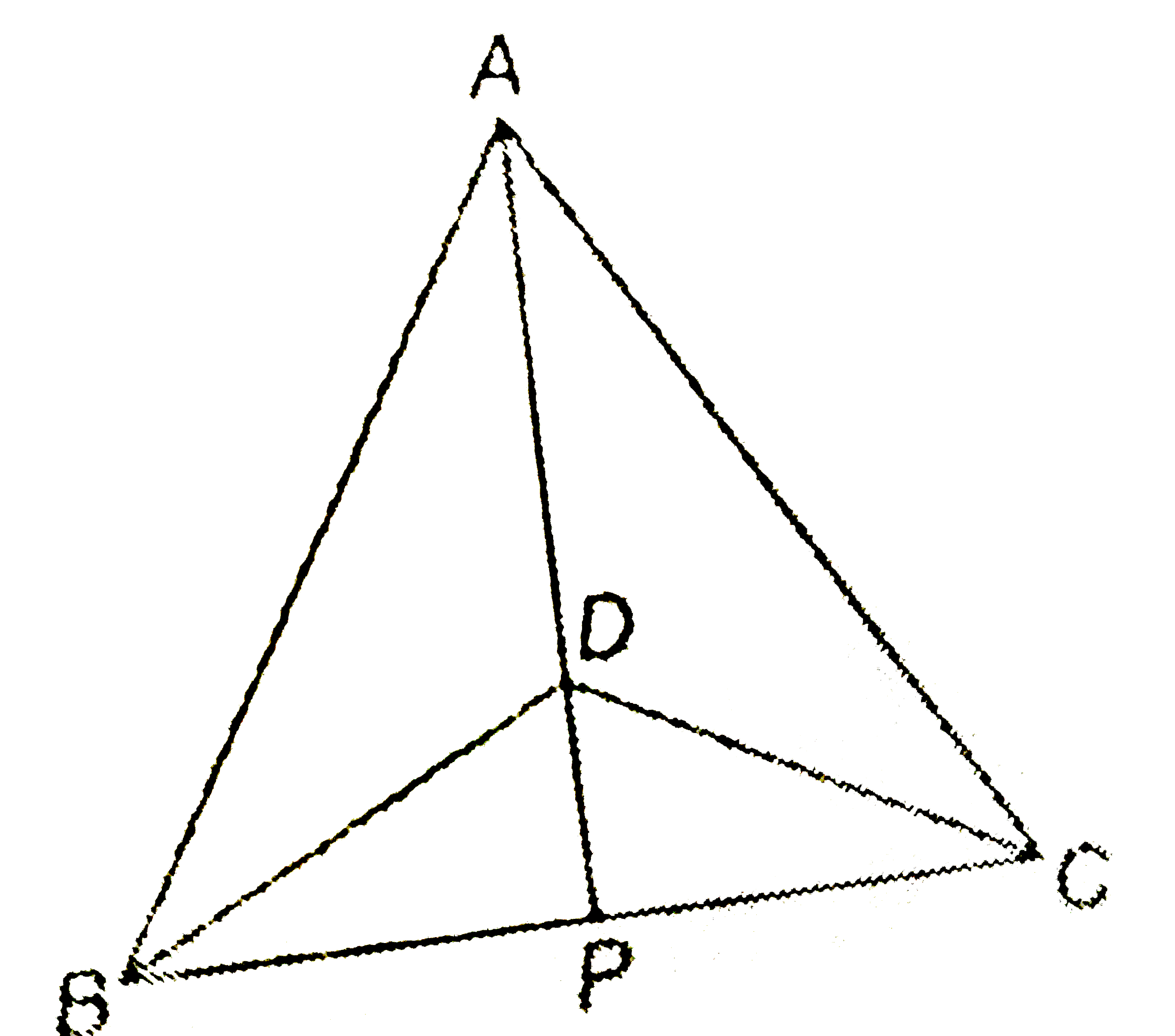
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
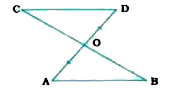
View SolutionLine segment AB is parallel to another line segment CD. O is the midpoint of AD (see the given figure). Show that
(i) △AOB=△DOC
(ii) O is also the midpoint of BC
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E, show that
(i) ΔABD≅ΔACD
(ii) ΔABE≅ΔACE
(iii) AE bisects ∠A as well as ∠D
(iv) AE is the perpendicualr bisector of BC.

View SolutionConsider two coherent sources S1andS2 producing monochromatic waves to produce interference patten. Let the displacement of the wave produced by S1 be given by
and the displacement by S2 be Y1=acosωt
Y2=acos(ωt−ϕ)
Find out expression for the amplitude of the resultant displacement at a point and show that the intensity at that point will be
I=4a2cos2ϕ/2
Hence establish the conditions for constructive and destructive interference.
(b) What is the effect on the interference friinges in Young's double slit experiment when (i) the width of the source slit is increased, (ii) the monochromatic source is replaced by a source is replaced by a source of white light ?
OR
(a) A ray, 'PQ' of light on the face AB of glass prism ABC (as shown in the figure) and emerges out of the face AC. Trace the path of the ray. Show that
∠i+∠e=∠A+∠δ
Where δ and e denote the angle of deviation and angle of emergence respectively.
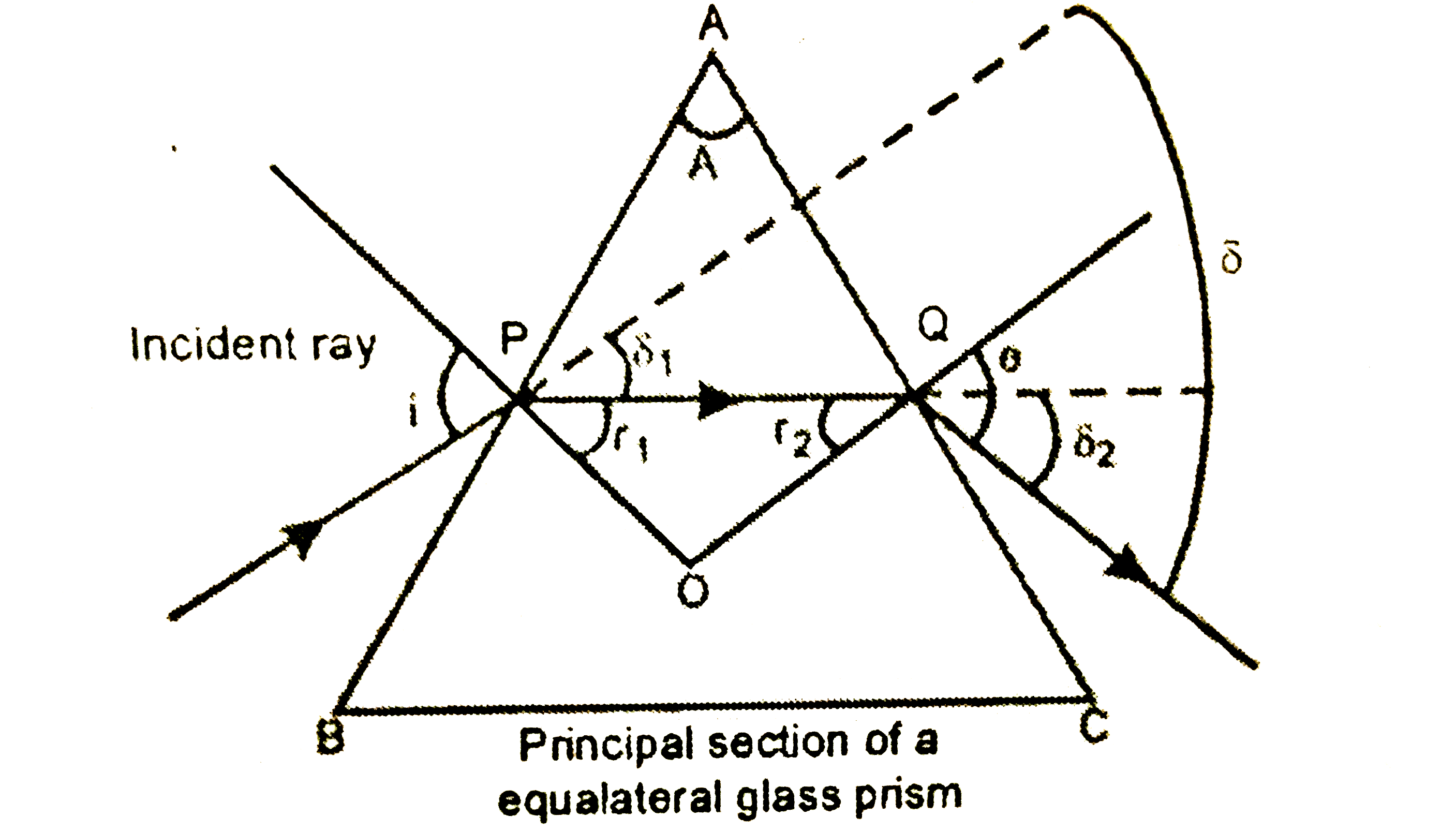
Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. state the condition under which ∠δ is minimum.
(b) Find out the relation between the refractive index (μ) of the glass prism and ∠A for the case when the angle of prism (A) is equal to the angle of minimum deviation (δm) . Hence obtain the value of the refractive index for angle Ae=60∘ .
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

View Solution(a) Draw the ray diagram showing refraction of ray of light through a glass prism. Derive the expression for the refractive index n of the material of prism in terms of the angle A ray angle of minimum deviation δm
(b) A ray of light PQ enters an isosceles right angles prism ABC of refractive index 1.5 as shown in figure .
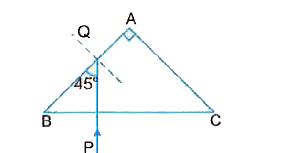
(i) Trace the path of the ray through the prism .
(ii) What will be the effect on the path of the ray if refractive index of the prism is 1.4 ?
View SolutionA student focussed the image of a candle flame on a white screen using a convex lens. He noted down the positive of the candle, screen and the lens as under.
Position of candle = 12.0 cm
Position of the screen = 50.0 cm
Position of the screen = 88.0 cm
(i) What is the focal length of the convex lens ?
(ii) Where will the image be formed if he shifts the candle towards the lens at a position of 31.0 cm ?
(iii) What will be the nature of the image formed if the further shifts the candle towards the lens ?
(iv) Draw a ray diagram to show the formation of the image in case (iii) as said above .
View SolutionA student focussed the image of a candle flame on a white screen using a convex lens. He noted down the position of the candle, screen and the lens as under
Position of candle =12.0cm
Position of convex lens =50.0cm
Position of the screen =88.0cm
(i) What is the focal length of the convex lens ?
(ii) Where will the image be formed if he shifts the candle towards the lens at a position of 31.0cm.
(iii) What will be the nature of the image formed if he further shifts the candle towards the lens ?
(iv) Draw a ray diagram to show the formation of the image in case (iii) as said above.
View Solution
