A region in electric field is specified by the potential function V(x)=4x2. Then, calcuate the magnitudes of electric field at distance x=2 m. Solution in Odia
Since, E=−dVdx
Given, potential function, V(x)=4x2
⇒ E=−dVdx=−ddx(4x2)=−8x
∴ Electric field at (x)=2⇒E=−16 V/m
Similar Questions
The electric potential V is givne as a function of distance x (metre) by V = (5 x^(2) + 10x - 9) volt. Value of electric field at x = 1 is
View SolutionThe electric potential V is givne as a function of distance x (metre) by V = (5 x^(2) + 10x - 9) volt. Value of electric field at x = 1 is
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
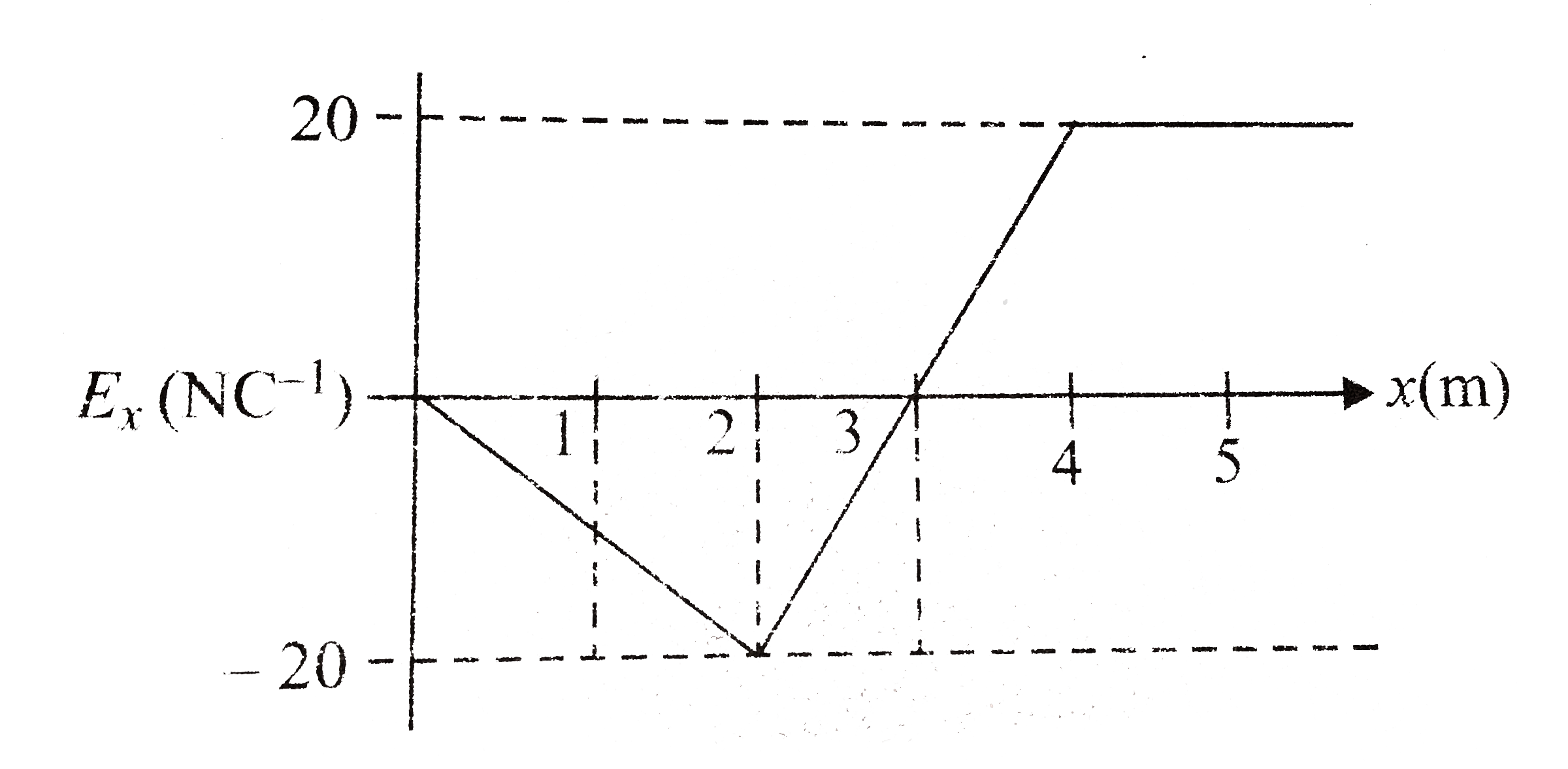
View SolutionThe electric potential V is given as a function of distance x (metre) by V = (6x^(2) + 10 x - 9) volt. Find magnitude of electric field (in V/m) at x= 4.
View SolutionA region in electric field is specified by the potential function V(x)= 4x^(2)
View SolutionA region is specified by the potential function V=2x2+3y2−5z2
Calculate the electric field strength at a point (2, 4,5) in this region.
View SolutionA region in electric field is specified by the potential function V(x)= 4x^(3) . Determine the electric field at the point x=1 located in the region.
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y- and z-components of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
View Solution
