Verify the Gauss' law for magnetic field of a point dipole of dipole moment M at the origin for the surface which is a sphere of radius R.
Text Solution
Let us draw the figure for given situation,
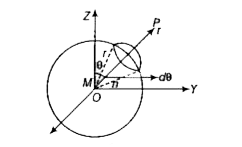
We have to prove that ∮B.dS=0. This is called Gauss law in magnetisation.
According to the question,
Magnetic moment of the dipole at origin O is
M=Mˆk
Let P be a point ar distance r from O and OP makes an angle θ with Z-axis.
Component of M along OP =Mcosθ
Now, the magnetic field induction at P due to dipole of moment Mcosθ is
B=μ04π.2Mcosθr3ˆi
From the diagram, r is the radius of sphere with centre at O lying in PZ-plane. Take an elementary area dS of the surface at P. Then,
dS=r(rsinθdθ)ˆr=r2sinθdθˆr
∮B.dS=∮μ04π.2Mcosθr3ˆr(r2sinθdθˆr)
=μ04π.Mr∫2π0sin2θdθ
=μ04π.Mr(−cos2θ2)2π0=−μ04π.M2r[cos4π−cosθ]
=μ04π.M2r[I−1]=0
|
Similar Questions
Verify the Gauss's law for magnetic field of a point dipole of dipole moment M at the origin for the surface which is a sphere of radius R.
View SolutionVerify the Gauss's law for magnetic field of a point dipole of dipole moment M at the origin for the surface which is a sphere of radius R.
View Solution
Knowledge Check
The magnetic field to a small magnetic dipole of magnetic moment M, at distance r from the centre on the equatorial line is given by (in M.K.S. system)
Aμ04π×Mr2Bμ04π×Mr3Cμ04π×2Mr2Dμ04π×2Mr3A bar magnet of length l and magnet dipole moment M is bent in the form of an arc. The new magnetic dipole moment is
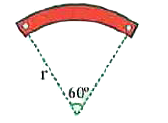 A3πMB2πMCM2DM
A3πMB2πMCM2DMThe electric field at a point on equatorial of a dipole and direction of the dipole moment
AWill be parallelBWill be in opposite directionCWill be perpendicularDAre not related
Dipole|| dipole moment|| field and potential due to dipole
View SolutionMagnetic moment and Magnetic Dipole moment
View SolutionMagnetic Dipole||Dipole Moment||Dipole in Magnetic Field
View SolutionThe electric field at a point on equatorial of a dipole and direction of the dipole moment
View SolutionA circular coil of radius r, and carrying a current I has a magnetic dipole moment M. What is its new dipole moment, if the radius of the coil is doubled and the current passing through the coil is halved?
View Solution
