A number of particles each of mass 10g are in motion. 20% of the particles have speed 10ms−1,50% of particles speed 30ms−1 and 30% have speed 40ms−1. Calculate the root mean square speed of the particles.
To calculate the root mean square (RMS) speed of the particles, we can follow these steps:
Step 1: Understand the distribution of speeds
We have particles with different speeds and their respective percentages:
- 20% of particles have a speed of 10 m/s
- 50% of particles have a speed of 30 m/s
- 30% of particles have a speed of 40 m/s
Step 2: Convert percentages to fractions
To make calculations easier, convert the percentages to fractions:
- 20% = 0.20
- 50% = 0.50
- 30% = 0.30
Step 3: Use the RMS speed formula
The formula for root mean square speed (vrms) is:
vrms=
⎷∑(fi⋅v2i)∑fi
where fi is the fraction of particles with speed vi.
Step 4: Calculate the contributions of each speed
Now, we will calculate the contributions of each speed:
- For the speed of 10 m/s:
f1=0.20,v1=10m/s⇒f1⋅v21=0.20⋅(10)2=0.20⋅100=20
- For the speed of 30 m/s:
f2=0.50,v2=30m/s⇒f2⋅v22=0.50⋅(30)2=0.50⋅900=450
- For the speed of 40 m/s:
f3=0.30,v3=40m/s⇒f3⋅v23=0.30⋅(40)2=0.30⋅1600=480
Step 5: Sum the contributions
Now, sum the contributions:
∑(fi⋅v2i)=20+450+480=950
Step 6: Calculate the total fraction
The total fraction of particles is:
∑fi=0.20+0.50+0.30=1.00
Step 7: Substitute into the RMS formula
Now, substitute these values into the RMS formula:
vrms=√9501.00=√950
Step 8: Calculate the final result
Now, calculate the square root:
vrms≈30.82m/s
Final Answer
The root mean square speed of the particles is approximately 30.82 m/s.
---
We have particles with different speeds and their respective percentages:
- 20% of particles have a speed of 10 m/s
- 50% of particles have a speed of 30 m/s
- 30% of particles have a speed of 40 m/s
To make calculations easier, convert the percentages to fractions:
- 20% = 0.20
- 50% = 0.50
- 30% = 0.30
The formula for root mean square speed (vrms) is:
vrms=
⎷∑(fi⋅v2i)∑fi
where fi is the fraction of particles with speed vi.
Now, we will calculate the contributions of each speed:
- For the speed of 10 m/s:
f1=0.20,v1=10m/s⇒f1⋅v21=0.20⋅(10)2=0.20⋅100=20
f2=0.50,v2=30m/s⇒f2⋅v22=0.50⋅(30)2=0.50⋅900=450
f3=0.30,v3=40m/s⇒f3⋅v23=0.30⋅(40)2=0.30⋅1600=480
Now, sum the contributions:
∑(fi⋅v2i)=20+450+480=950
The total fraction of particles is:
∑fi=0.20+0.50+0.30=1.00
Now, substitute these values into the RMS formula:
vrms=√9501.00=√950
Now, calculate the square root:
vrms≈30.82m/s
The root mean square speed of the particles is approximately 30.82 m/s.
Similar Questions
Knowledge Check
A body moving along a straight line travels one third of the total distance with a speed of 3.0ms−1. The remaining distance is covered with a speed of 4.0ms−1 for half the time and 5.0ms−1 for the other half of the time. The average speed during the motion is
A4.0ms−1B6.0ms−1C3.8ms−1D2.4ms−1
s-t graph of a particle in motion is shown in Fig. Calculate
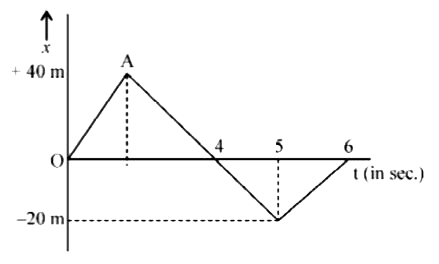
Average speed
View SolutionThe speed of six different molecules in a gas are 25ms−1,20ms−1,30ms−1,15ms−1,10ms−1 and 25ms−1. Calculate the average speed and also the root mean square of the gas.
View SolutionConsider an 1100 particels gas system with speeds distribution as follows :
1000 particles each with speed 100m/s
2000 particles each wityh speed 200m/s
4000 particles each with speed 300m/s
3000 particles each with speed 400m/s and 1000 particles each with speed 500m/s
Find the average speed, and rms speed.
View SolutionCalculate the pressure exerted by 1023 gas particles each of mass 10−22 g in a container of volume 1dm3. The root mean square speed is 105cms−1
View SolutionFour particles have velocities 1,0,2,and3m/s. The root mean square velocity of the particles (definition wise) is.
View SolutionAt a certain temperature 6% molecules of a gas have speed 2m/s, 9% have speed 3m/s, 30% have speed 9m/s, 28% have speed 11m/s, 20% have speed 13m/s and 7% have speed 18m/s. Calculate Ump,Uav and Urms at that temperature.
View SolutionA time varying force acts on a particle of mass 5 kg as shown in figure . Find the speed of the particle, in m/s , after 10 s , if particle was intially at rest .
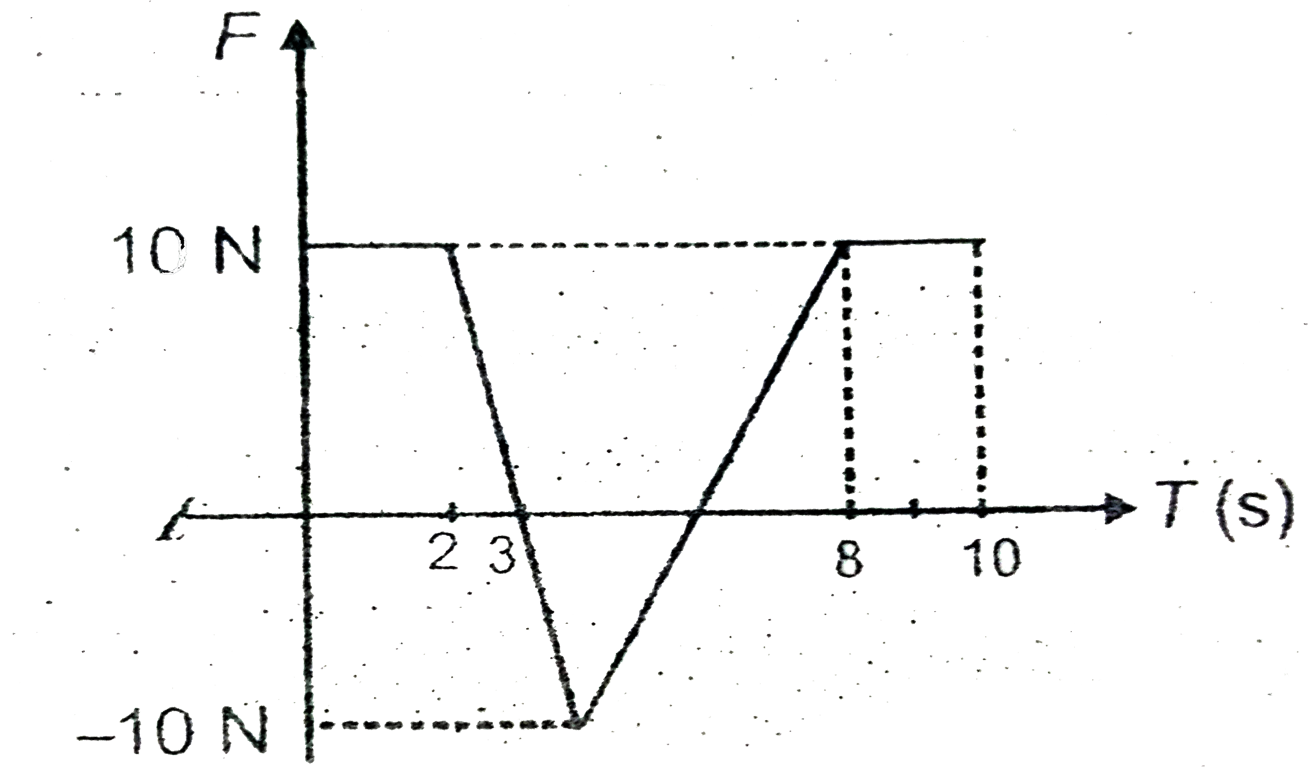
View Solution
