The molecular speeds of gaseous molecules are analogous to those to rifle bullets , why do then odour of the gaseous molecular not detected so fast ?
Step-by-Step Solution:
1. Understanding Molecular Speed: The question begins by comparing the speed of gaseous molecules to that of rifle bullets. Both can travel at high speeds, but the behavior of gaseous molecules is different due to their nature.
2. Path of Molecules: Unlike rifle bullets, which travel in a straight line, gaseous molecules do not maintain a straight path. This is primarily due to their interactions with other molecules in the air.
3. Collisions with Other Molecules: In a gaseous environment, there are many other gas molecules present. When a gaseous molecule moves, it frequently collides with these other molecules. These collisions alter the direction of the moving molecule.
4. Zigzag Motion: Due to these collisions, instead of moving in a straight line, gaseous molecules follow a zigzag or random path. This random motion means that the molecules take longer to reach our noses, which is why we do not detect the odor quickly.
5. Conclusion: The analogy of molecular speeds to rifle bullets is misleading in this context. While both can be fast, the zigzag path of gaseous molecules due to collisions with other molecules in the air slows down the detection of odors.
---
Similar Questions
Gaseous SO3 molecule
View SolutionAir consists mainly of nitrogen and oxygen molecules. Relative molecular masses of nitrogen and oxygen are 28 and 32 respectiely. Calculate :
(i) the ratio of the rms speed of nitrogen molecules to that of the oxygen molecules in air and
(ii) the ratio of the r.m.s. speed of oxygen molecules in air at 0∘C to that at 10∘C.
View SolutionAt what temperature is the "effective" speed of gaseous hydrogen molecules (molecular weight = 2) equal to that of oxygen molecules (molecular weight = 32) at 47∘C?
View SolutionWhat is the shape of SO3 molecule in gaseous state?
View SolutionUse molecular orbital theory to explain why the Be2 molecule does not exist.
View SolutionThe Earth's atmosphere consists primarily of oxygen (21%) and nitrogen (78%). The rms speed of oxygen molecules (O2) in the atmosphere at a certain location is 535 m/s. The rms speed of the nitrogen molecules at this location will be [Given 1 amu =1.66×10−26 kg, molecular mass of O2=32, molecular mass of N2=28]
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
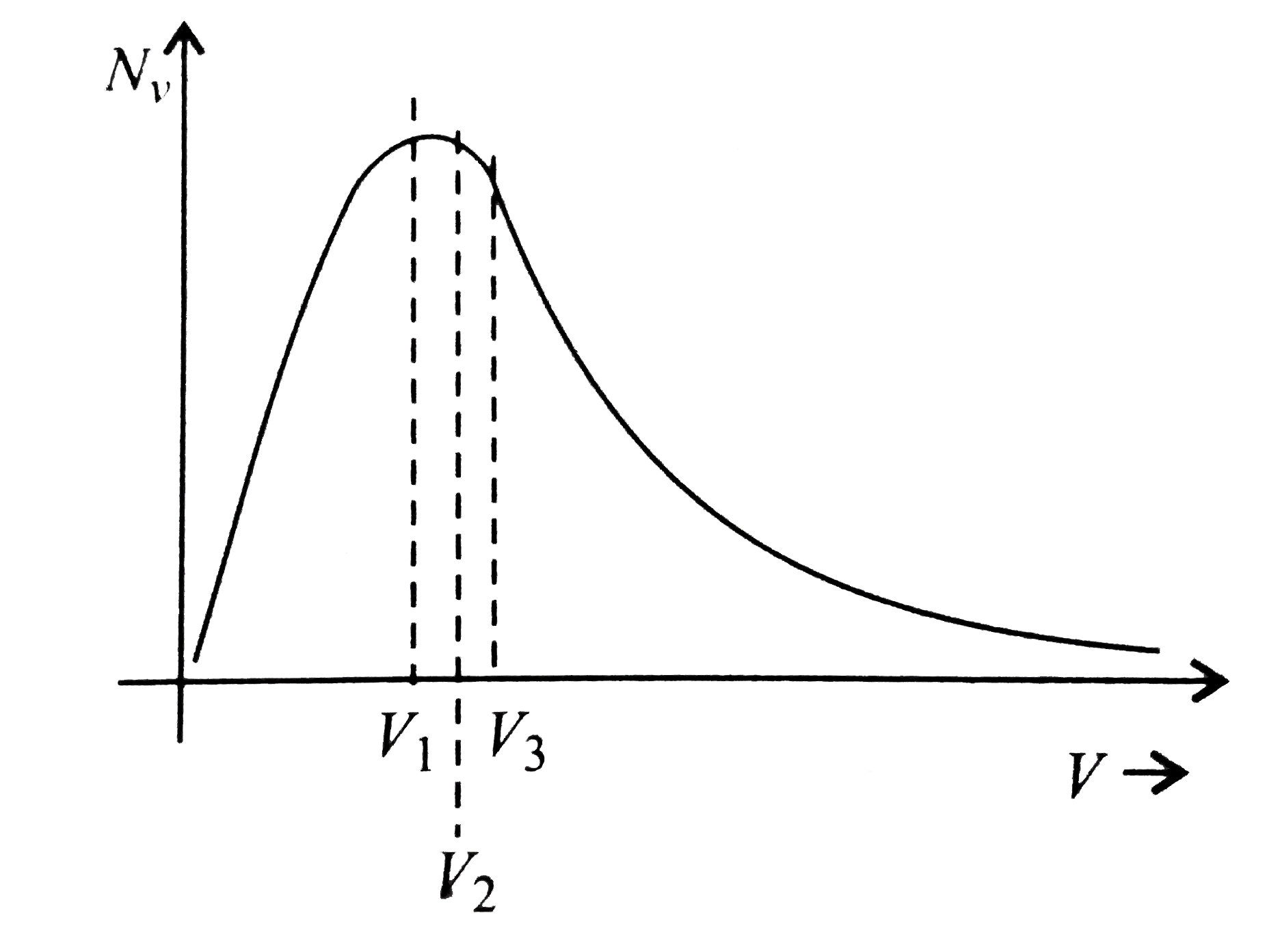
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of a are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
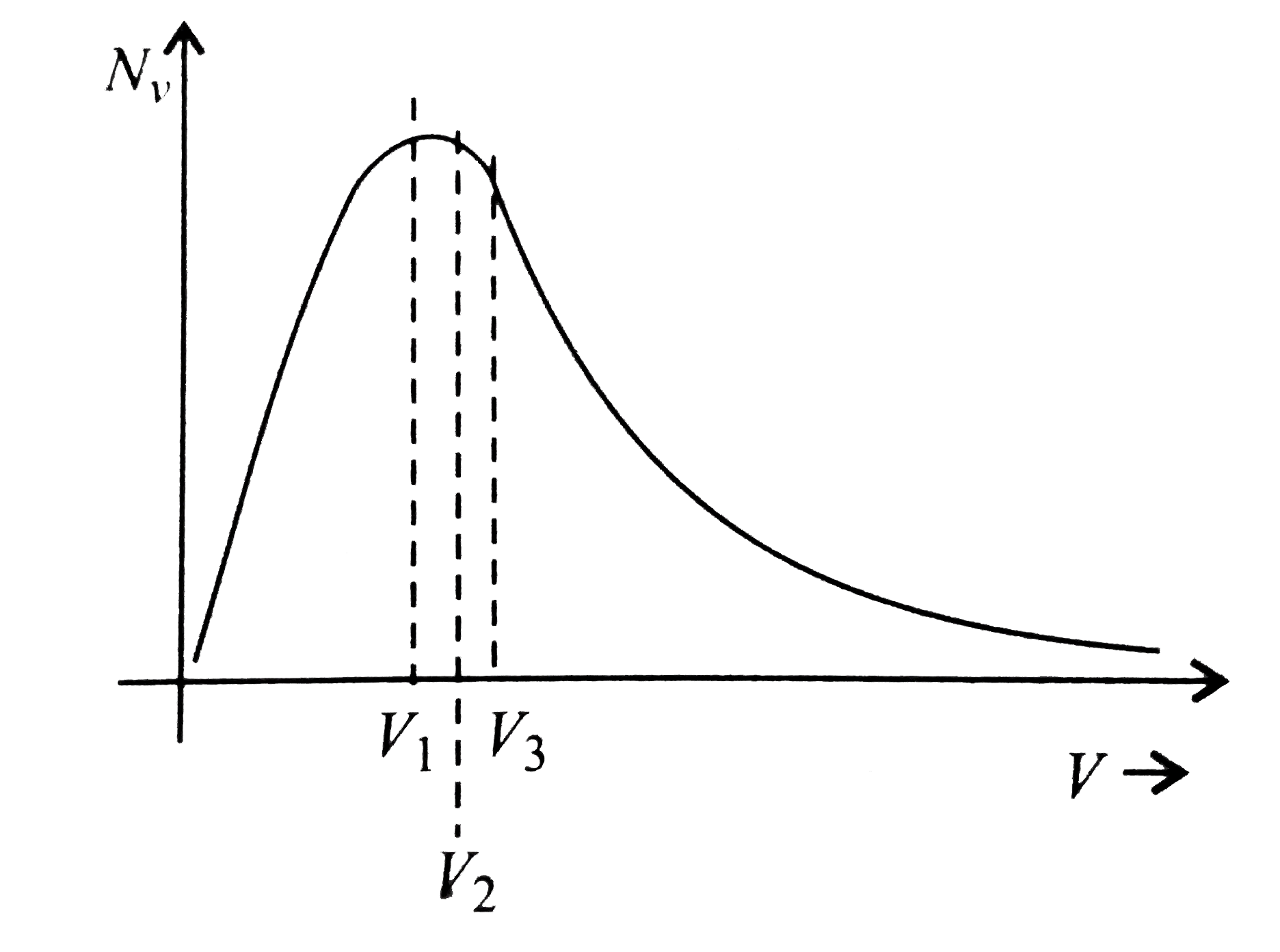
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b are
View SolutionAssertion : VrmsandVmean of gaseous molecules is nearly of the order of velocity of sound.
Reason : The sound travels in air because of vibrational molecular motion.
View SolutionAt what temperature in C the rms speed of gaseous hydrogen molecules equal to that of oxygen molecules at 79 C?
View Solution
