The equation. Δx.Δp≥h/4π shows
de-Broglie relation
Heisenberg's uncertainty principle
Aufbau principle
Hund's rule
The correct Answer is:B
To solve the question regarding the equation ΔxΔp≥h4π, we will analyze its significance in the context of quantum mechanics.
1. Identify the Variables:
- Δx: This represents the uncertainty in position.
- Δp: This represents the uncertainty in momentum.
- h: This is Planck's constant, which is a fundamental constant in quantum mechanics.
2. Understand the Equation:
- The equation ΔxΔp≥h4π is known as Heisenberg's Uncertainty Principle. It states that the product of the uncertainties in position and momentum of a particle cannot be smaller than h4π.
3. Interpret the Implications:
- This principle implies that the more precisely we know the position of a particle (i.e., the smaller Δx is), the less precisely we can know its momentum (i.e., the larger Δp becomes), and vice versa. This is a fundamental property of quantum systems.
4. Relate to Quantum Mechanics:
- In quantum mechanics, particles such as electrons do not have definite positions and momenta at the same time. This uncertainty is not due to measurement limitations but is intrinsic to the nature of quantum particles.
5. Conclusion:
- Therefore, the equation ΔxΔp≥h4π shows Heisenberg's Uncertainty Principle, which highlights the limitations in simultaneously knowing the position and momentum of a particle.
- Δx: This represents the uncertainty in position.
- Δp: This represents the uncertainty in momentum.
- h: This is Planck's constant, which is a fundamental constant in quantum mechanics.
- The equation ΔxΔp≥h4π is known as Heisenberg's Uncertainty Principle. It states that the product of the uncertainties in position and momentum of a particle cannot be smaller than h4π.
- This principle implies that the more precisely we know the position of a particle (i.e., the smaller Δx is), the less precisely we can know its momentum (i.e., the larger Δp becomes), and vice versa. This is a fundamental property of quantum systems.
- In quantum mechanics, particles such as electrons do not have definite positions and momenta at the same time. This uncertainty is not due to measurement limitations but is intrinsic to the nature of quantum particles.
- Therefore, the equation ΔxΔp≥h4π shows Heisenberg's Uncertainty Principle, which highlights the limitations in simultaneously knowing the position and momentum of a particle.
Similar Questions
It is impossible to determine simultaneously the position of velocity of small microscopic particle such as electron , proton or neutron with accuracy .This is called Heisenberg's uncertainty principle. Mathematically, it is represented as Δx.Δp≥h4π,Δx is uncertainty in position Δp is uncertainty in momentum.
View SolutionLet Δ denote the area of the ΔABCandΔp be the area of its pedal triangle. If Δ=kΔp, then k is equal to
View SolutionSTATEMENT-1 : Δx:Δp=h4π is not applicable for macroscope particles.
STATEMENT-2 : p,orbital is an example of gerade.
STATEMENT-3 : Due to production of matter waves, energy of the moving system decreases
View SolutionDerive the following equation :
ΔH=ΔU+(Δn)RT
View SolutionGiven that α, γ are roots of the equation Ax2−4x+1=0 and β, δ are roots of the equation Bx2−6x+1=0. If α, β,γ and δ are in H.P., then
View SolutionIf α,β,γ,δ are the roots of the equation x4+x2+1=0 then the equation whose roots are α2,β2,γ2,δ2 is
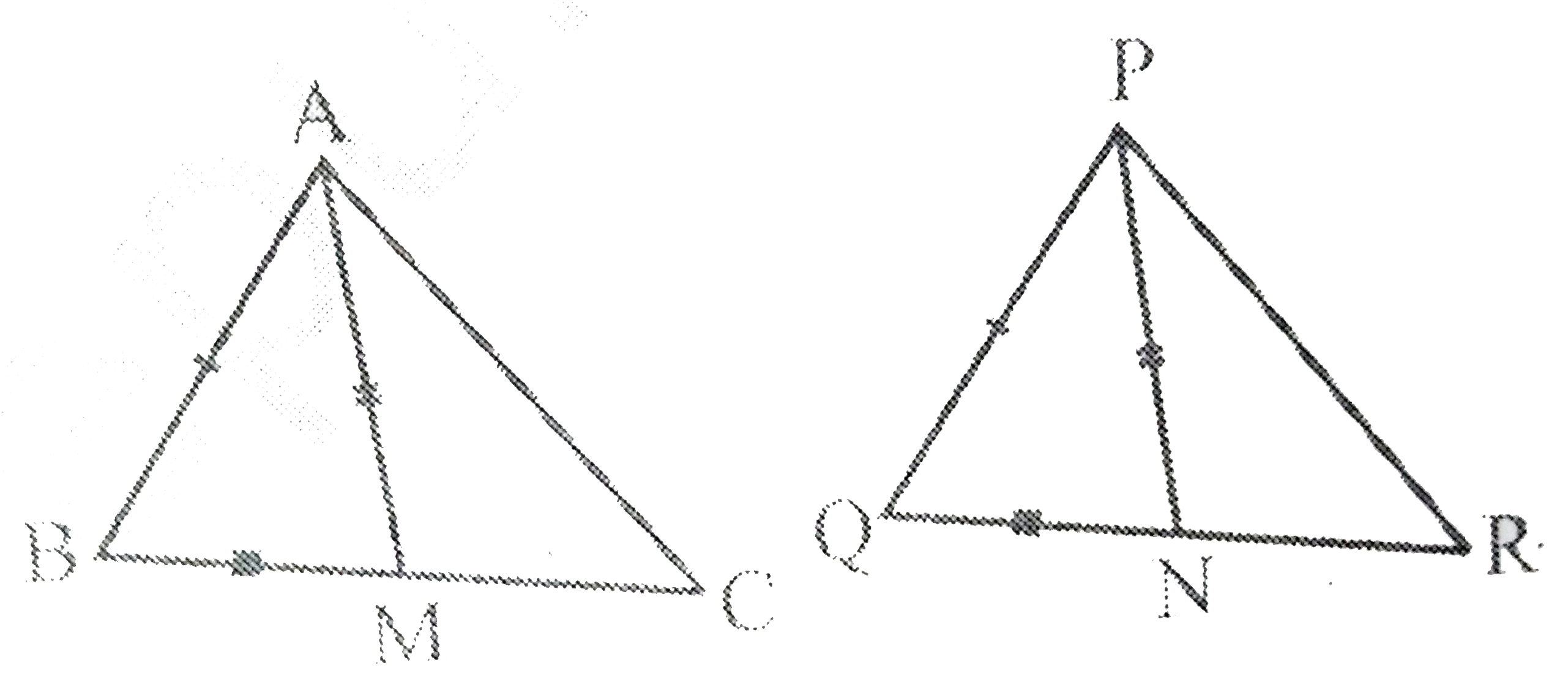
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
View SolutionThe number of values of x in [0,4π] satisfying the inequation ∣∣√3cosx−sinx∣∣≥2, is
View SolutionThe equation of S.H.M. of a particle is a+4π2x=0, where a is instantaneous linear acceleration at displacement x. Then the frequency of motion is
View SolutionGiven that α,γ are roots of the equation Ax2−4x+1=0,andβ,δ the roots of the equation of Bx2−6x+1=0, such that α,β,γ,andδ are in H.P., then a.A=3 b. A=4 B=2 d. B=8
View Solution
