Two sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
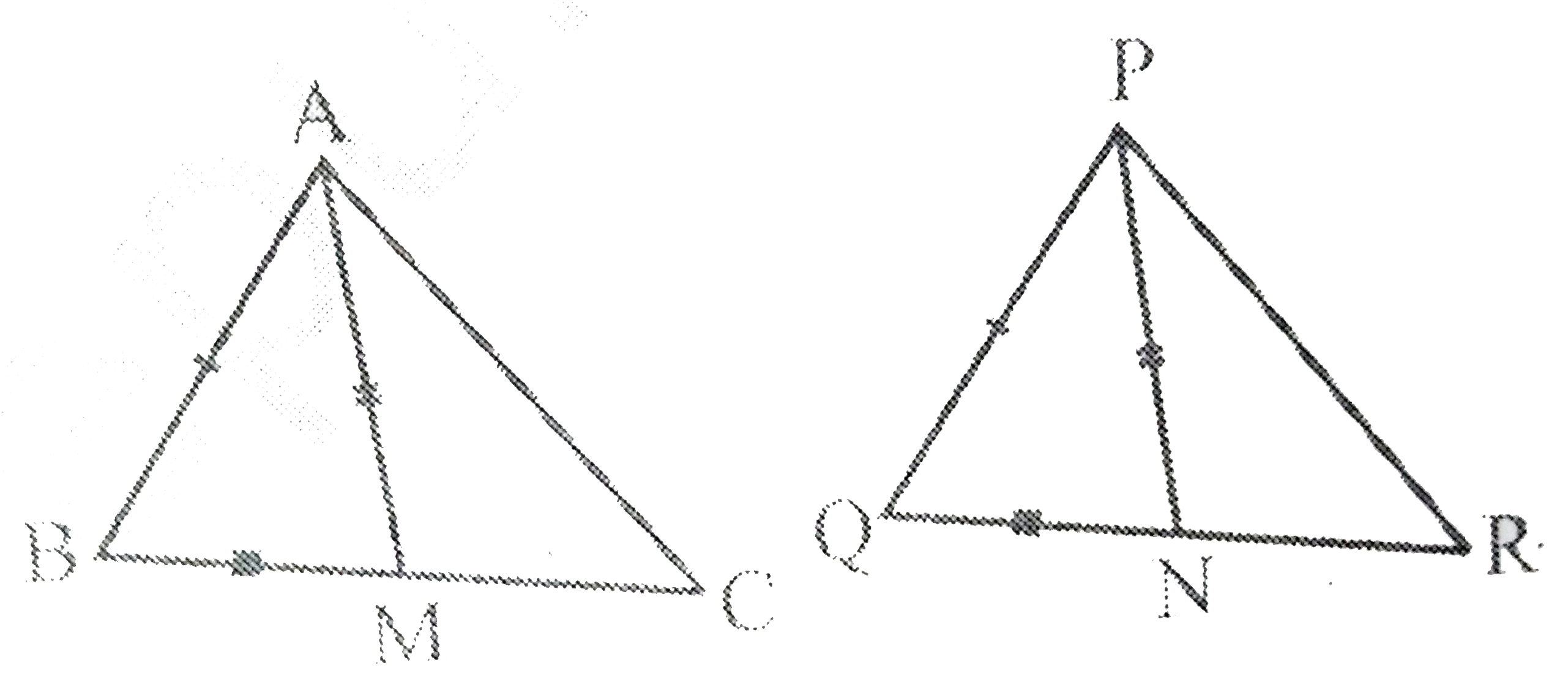
(##IX07_E0303_s01##)
In ΔABC, AM is the median to BC.
∴ BM=12BC
In ΔPQR, PN is the median to QR.
∴ QN=12QR
It is given thatBC=QR
∴12BC=12QR
∴BM=QN … (1)
In ΔABM and ΔPQN,
AB=PQ (Given)
BM=QN [From equation (1)]
AM=PN (Given)
∴ ΔABM≅ΔPQN (Using SSS congruence criterion)
⇒∠ABM=∠PQN (By CPCT)
⇒∠ABC=∠PQR … (2)
(ii) In Δ ABC and Δ PQR ,
AB=PQ (Given)
∠ABC=∠PQR [From Equation (2)]
BC=QR (Given)
∴ ΔABC≅ΔPQR (By SAS congruence rule)
Similar Questions
Two sides AB and BC and median AD of triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR. Show that:
ΔABD=ΔPQN
View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
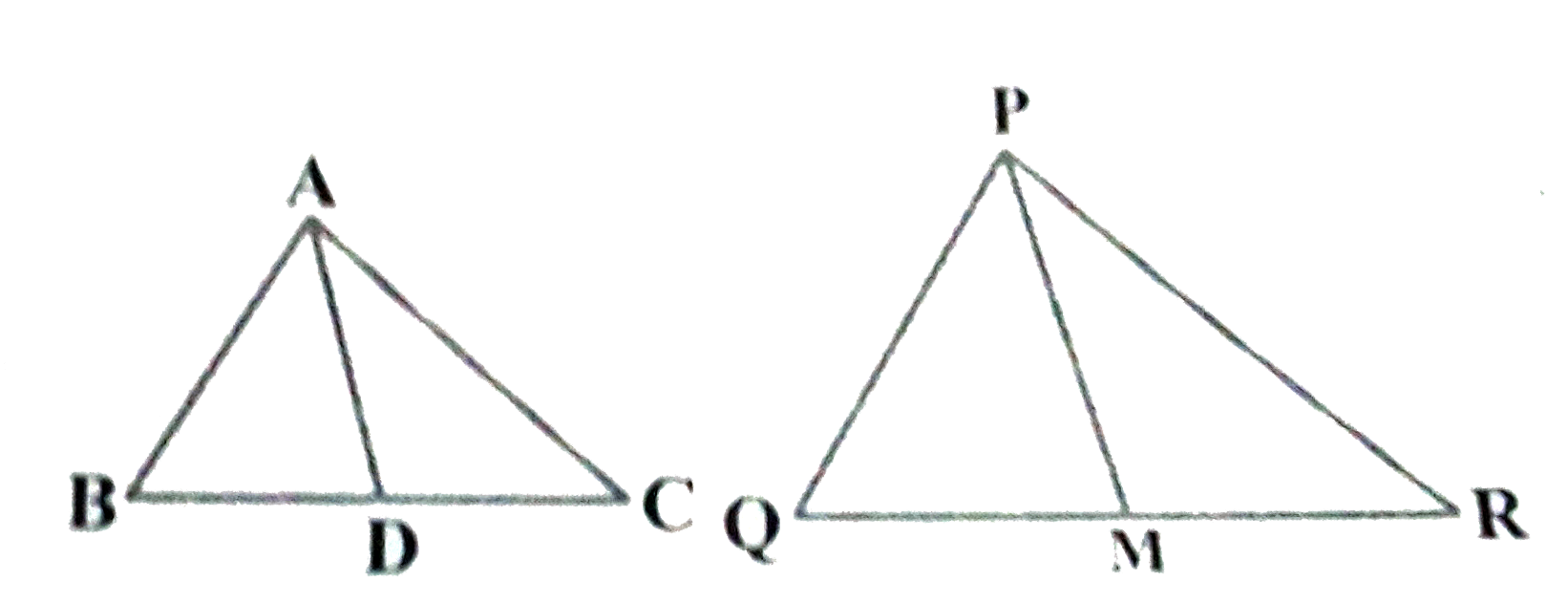
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC~ΔPQR.
View SolutionIn the following figures, the sides AB and BC and the median AD of triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that ΔABCandΔPQR are congruent.

View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionIn Figure, two sides AB and BC and the median AD of ABC are equal respectively to the two sides PQ and QR and the median PM of the other triangle PQR. Prove that ABD≅PQM (ii) ABC ≅ PQR
View SolutionIn figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that: (i) ΔAMC~ΔPNR (ii) CMRN=ABPQ (ii) ΔCMB~ΔRNQ
View SolutionABandCD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50). Show that ∠A>∠C and ∠B>∠D.

View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
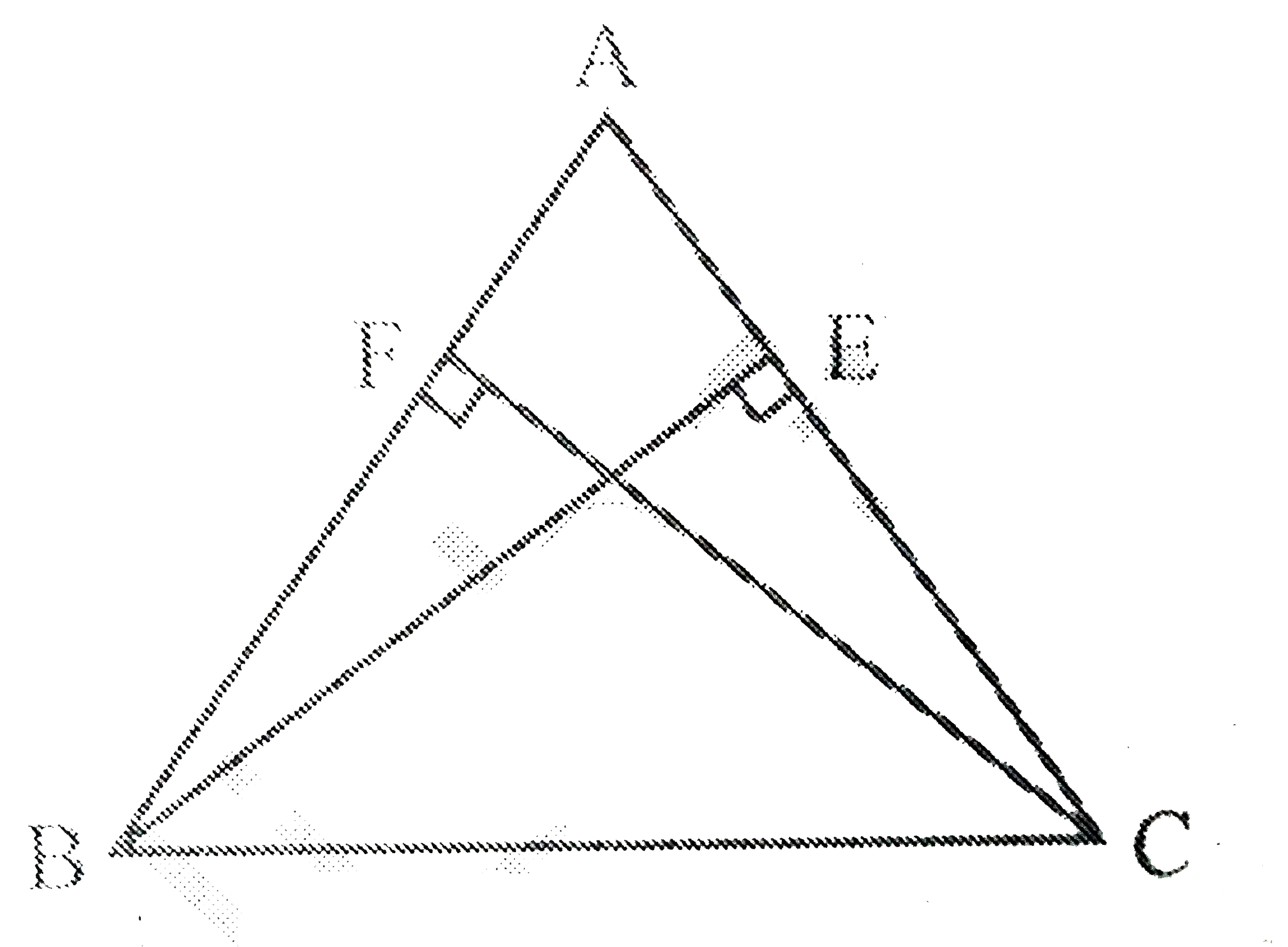
View Solution