In two containers X and Y same gas is filled. If the pressure, volume and absolute temperature of gas in X are three times as compared to that in Y and if the mass of X is mg, the mass of Y is
mg
m/3g
m/2g
2mg
The correct Answer is:B
To solve the problem, we will use the ideal gas equation and the relationships given in the question. Let's break it down step by step.
Step 1: Write down the ideal gas equation
The ideal gas equation is given by:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles
- R = universal gas constant
- T = absolute temperature
Step 2: Relate moles to mass
The number of moles n can also be expressed as:
n=mM
where:
- m = mass of the gas
- M = molar mass of the gas
Step 3: Set up equations for containers X and Y
For container X:
- Pressure: Px=3Py
- Volume: Vx=3Vy
- Temperature: Tx=3Ty
- Mass: mx=mg
For container Y, we need to find the mass my.
Step 4: Write the ideal gas equation for both containers
For container X:
PxVx=nxRTx
Substituting the values:
(3Py)(3Vy)=mxMR(3Ty)
This simplifies to:
9PyVy=mgMR(3Ty)
For container Y:
PyVy=nyRTy
Substituting the values:
PyVy=myMRTy
Step 5: Divide the equations
Now, we will divide the equation for container X by the equation for container Y:
9PyVyPyVy=mgMR(3Ty)myMRTy
This simplifies to:
9=mg⋅3my
Step 6: Solve for my
Rearranging the equation gives:
my=mg⋅39
This simplifies to:
my=mg3
Final Answer
The mass of gas in container Y is:
my=mg3
The ideal gas equation is given by:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles
- R = universal gas constant
- T = absolute temperature
The number of moles n can also be expressed as:
n=mM
where:
- m = mass of the gas
- M = molar mass of the gas
For container X:
- Pressure: Px=3Py
- Volume: Vx=3Vy
- Temperature: Tx=3Ty
- Mass: mx=mg
For container X:
PxVx=nxRTx
Substituting the values:
(3Py)(3Vy)=mxMR(3Ty)
This simplifies to:
9PyVy=mgMR(3Ty)
PyVy=nyRTy
Substituting the values:
PyVy=myMRTy
Now, we will divide the equation for container X by the equation for container Y:
9PyVyPyVy=mgMR(3Ty)myMRTy
This simplifies to:
9=mg⋅3my
Rearranging the equation gives:
my=mg⋅39
This simplifies to:
my=mg3
The mass of gas in container Y is:
my=mg3
Similar Questions
Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas is container B is compressed to half of its original vlue adiabatically. The ratio of final pressure of gas of B to that of gas in A is
View SolutionA gas is filled in a container at certain temperature and pressure. At the same temperature more gas is filled in the vessel. Calculate the percentage increase in the mass of the gas. If the ratio of initial and final pressure is 1:2.
View Solution
Knowledge Check
Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is
A2γ−1B1(2)γ−1C1(1−γ)2D1(γ−1)2
A gas is filled in a container at certain temperature and pressure. At the same temperature more gas is filled in the vessel. Calculate the percentage increase in the mass of the gas. If the ratio of initial and final pressure is 1:2.
View SolutionA gas is undergoing an adiabatic process. At a certain stage, the volume and absolute temperature of the gas are V0,T0 and the magnitude of the slope of the V-T curve is m. molar specific heat of the gas at constant pressure is [Assume the volume of the gas is taken on the y-axis and absolute temperature of the gas taken on x-axis]
View SolutionA given sample of an ideal gas occupise a volume V at a pressure p and absolute temperature T.The mass of each molecule of the gas is m. Which of the following is the density of the gas ?
View SolutionFor a given mass of gas the variation of pressure versus temperature is shown in the figure. What is the ratio of volume of the gas at points A and B.
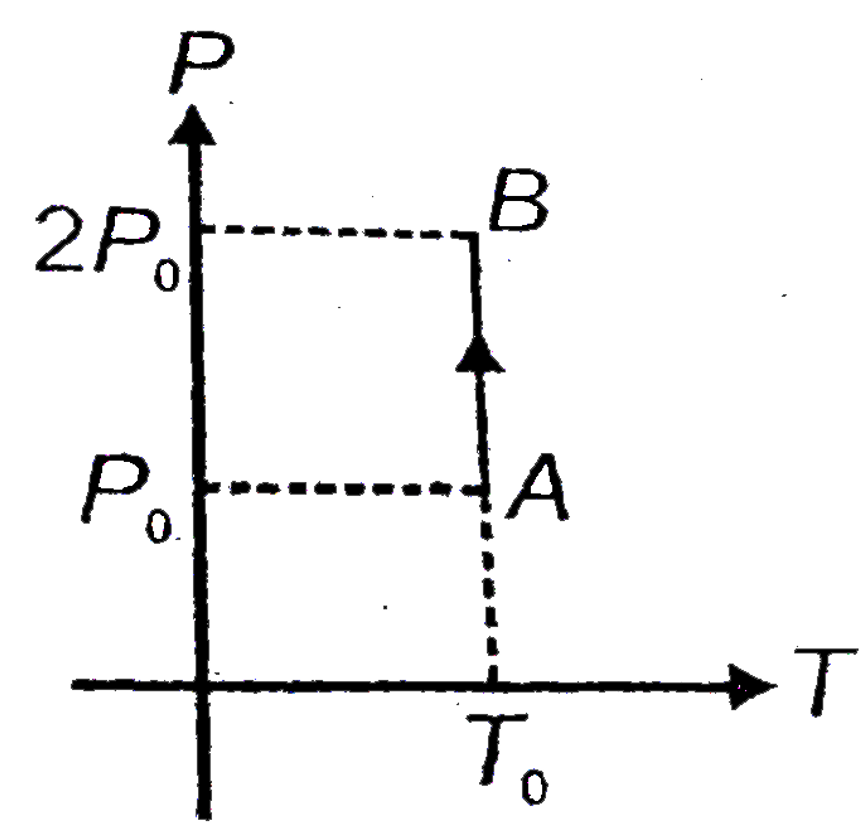 .
.
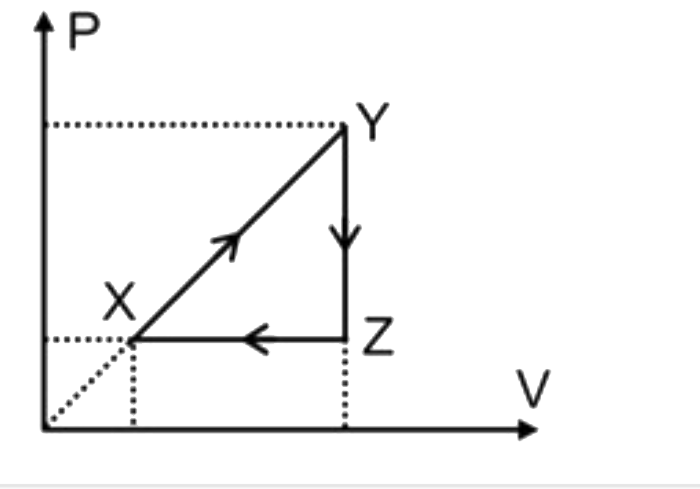
View SolutionIn the show indicator diagram over pressure - volume scales 'n' moles of an ideal gas is cycled . If the temperature of the gas in the state X and Y are respectively TXandTY . Temperature of the gas in the state Z is the (All temperature are in absolute scale )
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View Solution
