A large cylinder of helium filled at 1000 pascal had a thin orifice through which helium escaped into an evacuated space at the rate of 6.4 m mol/h. How long would it take for 10 m mol SO2 to leak through a similar orific if the SO2 were confined at the same pressure ?
6.25 h
0.39 h
4.42 h
1.00 h
The correct Answer is:A
To solve the problem, we need to determine how long it would take for 10 m mol of sulfur dioxide (SO₂) to leak through an orifice, given the rate at which helium (He) escapes through a similar orifice.
1. Identify Given Data:
- Rate of helium escape (R₁) = 6.4 m mol/h
- Molar mass of helium (M₁) = 4 g/mol
- Molar mass of sulfur dioxide (M₂) = 64 g/mol
- Amount of SO₂ to leak = 10 m mol
2. Apply Graham's Law of Effusion:
According to Graham's law, the rates of effusion of two gases are inversely proportional to the square root of their molar masses:
R₁R₂=√M₂M₁
Here, R₂ is the rate of SO₂ escape that we need to find.
3. Substitute Known Values:
6.4R₂=√644
Simplifying the right side:
√644=√16=4
So, we have:
6.4R₂=4
4. Solve for R₂:
Rearranging the equation gives:
R₂=6.44=1.6 m mol/h
5. Calculate Time Required for SO₂ to Leak:
We need to find out how long it takes for 10 m mol of SO₂ to leak at the rate of 1.6 m mol/h:
Time=Amount of SO₂R₂=10 m mol1.6 m mol/h=6.25 hours
Final Answer:
It would take 6.25 hours for 10 m mol of SO₂ to leak through the orifice.
---
- Rate of helium escape (R₁) = 6.4 m mol/h
- Molar mass of helium (M₁) = 4 g/mol
- Molar mass of sulfur dioxide (M₂) = 64 g/mol
- Amount of SO₂ to leak = 10 m mol
According to Graham's law, the rates of effusion of two gases are inversely proportional to the square root of their molar masses:
R₁R₂=√M₂M₁
Here, R₂ is the rate of SO₂ escape that we need to find.
6.4R₂=√644
Simplifying the right side:
√644=√16=4
So, we have:
6.4R₂=4
Rearranging the equation gives:
R₂=6.44=1.6 m mol/h
We need to find out how long it takes for 10 m mol of SO₂ to leak at the rate of 1.6 m mol/h:
Time=Amount of SO₂R₂=10 m mol1.6 m mol/h=6.25 hours
It would take 6.25 hours for 10 m mol of SO₂ to leak through the orifice.
Similar Questions
A cylindrical block of length 0.4 m and area of cross-section 0.04m2 is placed coaxially on a thin metal disc of mass 0.4 kg and of the same cross - section. The upper face of the cylinder is maintained at a constant temperature of 400 K and the initial temperature of the disc is 300K. if the thermal conductivity of the material of the cylinder is 10watt/m−K and the specific heat of the material of the disc is 600J/kg−K, how long will it take for the temperature of the disc to increase to 350 K? Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to be thermally insulated except for the upper face of the cylinder.
View SolutionA cylindrical tube with a frictionless piston ends in a small hole of area of cross–section 2×10−6m2, which is very small as compared to the area of cross-section of the tube. The tube is filled with a liquid of density 104kg/m3. The tube is held horizontal and the piston is pushed at a constant speed so that liquid comes out of the hole at a constant rate 'Q'm3/s. No liquid leaks around the piston. The material of the tube can bear a maximum pressure 6×105 Pa. The maximum possible value of Q so that the tube does not break is __________ ×10−5m3/s. [Atmospheric pressure =105 Pa]

View SolutionLiquid water coats an active (growing) icicle and extends up a short, narrow tube along the central axis. Because the water-ice interface must have a temperature of 0∘C, the water in the tube cannot lose energy through the sides of the icicle or down through the tip because there is no temperature change in those directions . It can lose energy and freeze only by sending energy up(through distance L) to the top of the icicle, where the temperature Tr can be below 0∘C. Take L=0.10m and Tr=−5∘C.Assume that the central tube and the upward conduction path both have crosse-sectional area A=0.5m2. The thermal conductivity of ice is 0.40 W/m⋅K, latent heat of fusion is LF=4.0×105J/K and the density of liquid water is 1000 kg/m3.
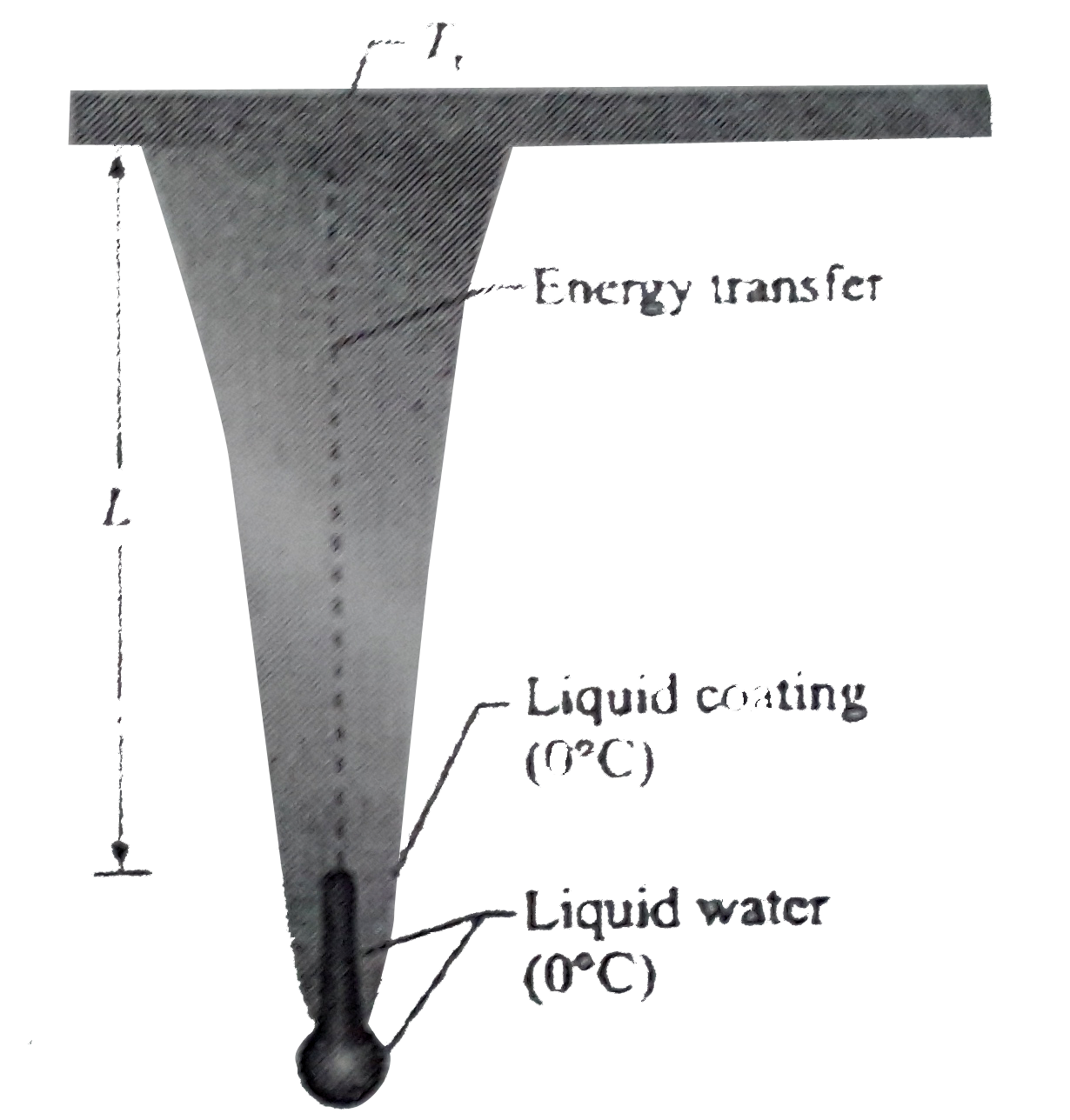
The rate at which mass converted from liquid to ice at the top of the central tube is
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
A small sphere of mass 2.00 g is released from rest in a large vessel filled with oil. The sphere approaches a terminal speed of 10.00 cm/s. Time required to achieve speed 6.32 cm/s from start of the motion is (Take g=10.00m/s2) :
View SolutionA farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
View SolutionA farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area 4×10−3m2. The spring is, initially in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does 50J of work in moving the piston through a distance 0.10m. The temperature of the gas increases by 50K. Calculate the spring constant and the heat supplied by the heater. Patm=1×105N/m2R=8.314J/mol−K
View SolutionA 3.6m long vertical pipe resonates with a source of frequency 212.5Hz when water level is at certain height in the pipe. Find the height of water level (from the bottom of the pipe) at which resonance occurs. Neglect end correction. Now , the pipe is filled to a height H(≈3.6m). A small hole is drilled very close to its bottom and water is allowed to leak. Obtain an expression for the rate of fall of water level in the pipe as a function of H. If the radii of the pipe and the hole are 2×10−2m and 1×10−3m respectively, Calculate the time interval between the occurance of first two resonances. Speed of sound in air 340m/s and g=10m/s2.
View SolutionA family enters a winter vacation cabin whose walls are adiabatic, initially the interior temperature is the same as the outside temperature (0∘C). The cabin consists of a single room of floor area 6m by 4m and height 3m. The room contains a 2kW electric heater. Assuming that the room is perfectly airlight and that all the heat from the heater is absorbed by the air, none escaping through the walls. The time after the heater is turned on, the air temperature reaches the comfort level of 21∘C in x×100sec, then find x (Take Cv=20.8J/mol−K)
View SolutionA very large metal plate carries a charge of Q=−1C. The work function for the metal is ϕ=3eV The plate is illuminated by a 60 watt light source with a wavelength λ of 330nm. How long does it take to completely discharge the plate? (Assume that every efficient photon ejects electron which is instantly removed from the sheet surface. (All photons ejected from light source fall normally on the metal plate) (h=6.6×10−34m2kg/s)
View Solution
