Chord AB of a circle is produced to a point P, and C is a point on the circle such that PC is a tangent to the circle. If PC = 18 cm, and BP = 15 cm, then AB is equal to:
6.2 cm
8.5 cm
5.8 cm
6.6 cm
To solve the problem, we will use the relationship between the tangent and the secant segments of a circle. The key formula we will use is:
PC2=PA×PB
Where:
- PC is the length of the tangent from point P to point C on the circle.
- PA is the length from point P to point A on the chord AB.
- PB is the length from point P to point B on the chord AB.
1. Identify the given values:
- PC=18 cm
- BP=15 cm
2. Calculate PC2:
PC2=182=324 cm2
3. Use the formula PC2=PA×PB:
324=PA×15
4. Solve for PA:
PA=32415=21.6 cm
5. Relate PA to PB and AB:
Since PA=PB+AB, we can express AB as:
AB=PA−PB
6. Substitute the known values:
AB=21.6−15
7. Calculate AB:
AB=6.6 cm
Final Answer:
Thus, the length of chord AB is 6.6 cm.
---
- PC is the length of the tangent from point P to point C on the circle.
- PA is the length from point P to point A on the chord AB.
- PB is the length from point P to point B on the chord AB.
- PC=18 cm
- BP=15 cm
PC2=182=324 cm2
324=PA×15
PA=32415=21.6 cm
Since PA=PB+AB, we can express AB as:
AB=PA−PB
AB=21.6−15
AB=6.6 cm
Thus, the length of chord AB is 6.6 cm.
Topper's Solved these Questions
Similar Questions
Chord AB of a circle is produced to a point P, and C is a point on the circle such that PC= 12cm, and BP = 10cm, then the length of AB (in cm ) is:
किसी वृत्त का जीवा ७8 को एक बिंदु P तक बढ़ाया जाता है, और C वृत्त पर एक बिंदु इस प्रकार है की PC=12cm, और BP = 10cm, फिर AB की लंबाई (सेमी में) है
View SolutionDraw a circle of radius 3 cm. Take a point P on the circle. At point P, construct a tangent to the circle.
View Solution
Knowledge Check
Chord AB of a circle is product to a point P and C is a poimt on the circle such that PC is a tangent to the circle. If PC = 18 cm, and BP = 15 cm, then AB is equal to:
A8.5 cmB6.2 cmC5.8 cmD6.6 cmChords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm, AP = 4 cm and PC = 5 cm, then CD is equal to:
A4.8 cmB6.8 cmC9.8 cmD7.8 cmTwo chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?A15.8 cmB12 cmC14 cmD14.6 cm
AB is a chord of a circle with O as centre. C is a point on the circle such that OC is perpendicular to AB and OC intersects AB at P. If PC = 2 cm and AB = 6 cm then the diameter of the circle is
View SolutionIn the given figure, TB is a chord which passes through the centre of the circle. PT is a tangent to the circle at the point T on the circle. If PT = 10 cm, PA = 5 cm and AB = x cm. then the radius of the circle is:
View SolutionVinod have 20 rupees. He bought 1, 2, 5 rupee stamps. They are different in numbers by the reason of no change, the shop keeper gives 3 one rupee stamps. So how many stamps Vinod have ?
View SolutionAB is a chord to a circle and PAT is the tangent to the circle at A. If ∠BAT=75∘and∠BAC=45∘, C being a point on the circle, then ∠ABC is equal to
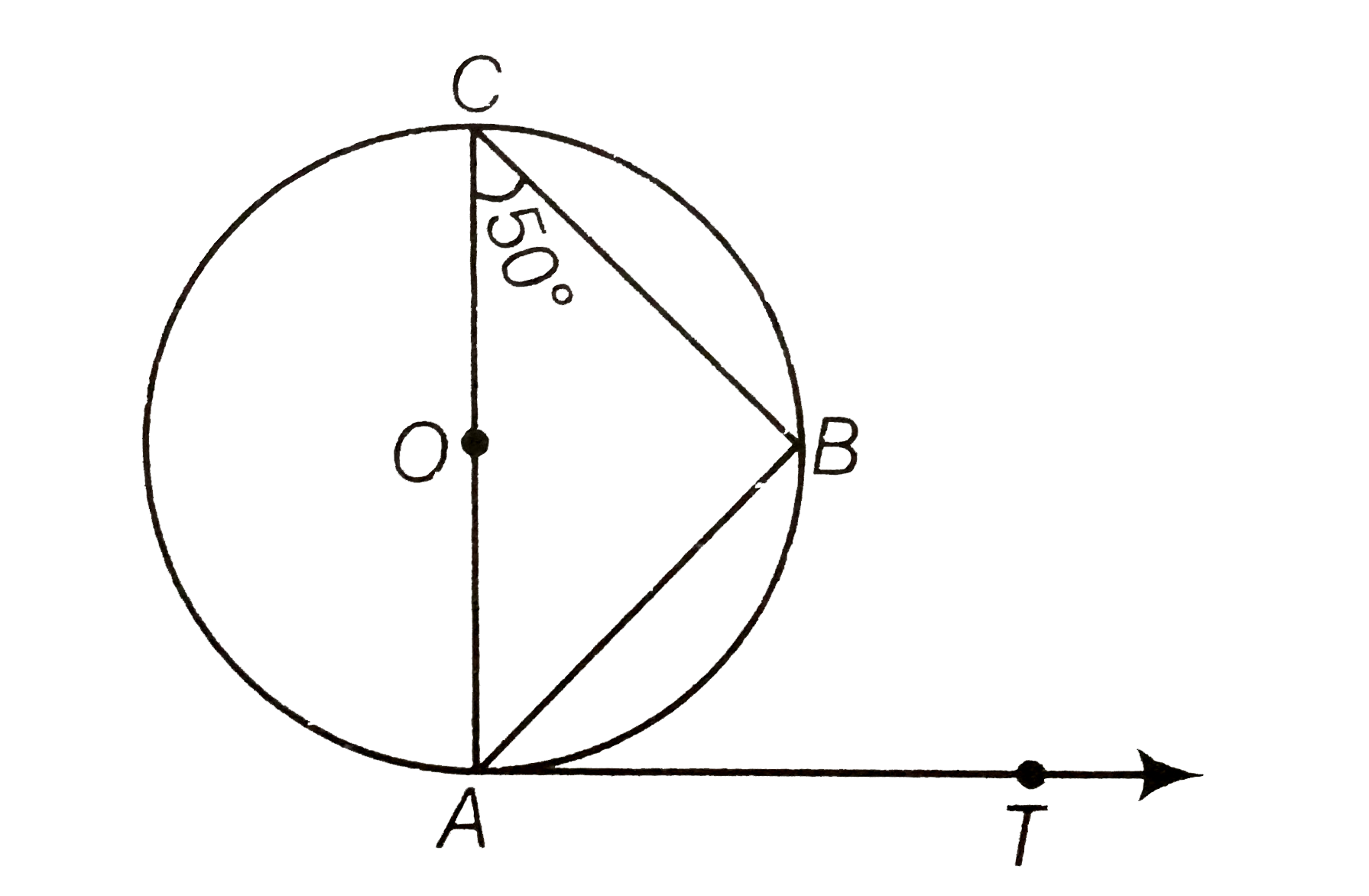
View SolutionIn figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
View Solution
