AB is a chord to a circle and PAT is the tangent to the circle at A. If ∠BAT=75∘and∠BAC=45∘, C being a point on the circle, then ∠ABC is equal to
40∘
45∘
60∘
70∘
The correct Answer is:C
To solve the problem, we need to find the angle ∠ABC given the following information:
- ∠BAT=75∘ (the angle between the chord AB and the tangent at point A)
- ∠BAC=45∘ (the angle between the chord AB and the line AC, where C is a point on the circle)
1. Identify the Angles:
- We have ∠BAT=75∘.
- We have ∠BAC=45∘.
2. Use the Alternate Segment Theorem:
- According to the Alternate Segment Theorem, the angle formed between a chord and a tangent at the point of contact is equal to the angle in the alternate segment.
- Therefore, ∠BCA=∠BAT=75∘.
3. Calculate the Third Angle in Triangle ABC:
- In triangle ABC, we know two angles:
- ∠BAC=45∘
- ∠BCA=75∘
- We can find the third angle ∠ABC using the fact that the sum of angles in a triangle is 180∘:
∠ABC=180∘−∠BAC−∠BCA
∠ABC=180∘−45∘−75∘
∠ABC=180∘−120∘
∠ABC=60∘
4. Conclusion:
- Therefore, the angle ∠ABC is 60∘.
Final Answer:
∠ABC=60∘
- ∠BAC=45∘ (the angle between the chord AB and the line AC, where C is a point on the circle)
- We have ∠BAT=75∘.
- We have ∠BAC=45∘.
- According to the Alternate Segment Theorem, the angle formed between a chord and a tangent at the point of contact is equal to the angle in the alternate segment.
- Therefore, ∠BCA=∠BAT=75∘.
- In triangle ABC, we know two angles:
- ∠BAC=45∘
- ∠BCA=75∘
- We can find the third angle ∠ABC using the fact that the sum of angles in a triangle is 180∘:
∠ABC=180∘−∠BAC−∠BCA
∠ABC=180∘−45∘−75∘
∠ABC=180∘−120∘
∠ABC=60∘
- Therefore, the angle ∠ABC is 60∘.
∠ABC=60∘
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
In figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View SolutionIn fig AB is chord of a circle with centre O and AP is the tangent at A such that ∠BAP=75∘ find ∠ACB
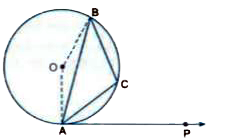
View Solution
Knowledge Check
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
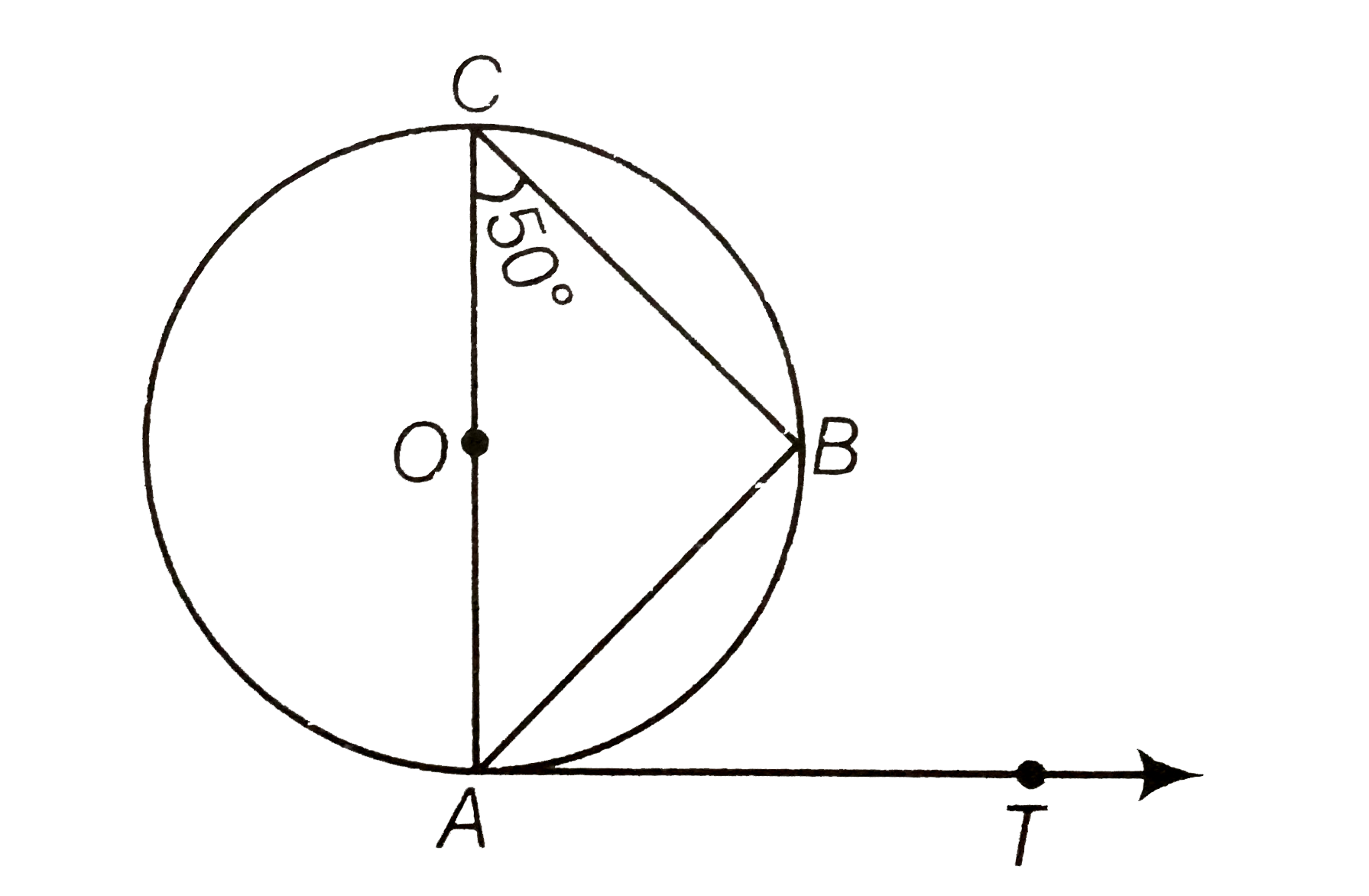 A45∘B60∘C50∘D55∘
A45∘B60∘C50∘D55∘Chord AB of a circle is product to a point P and C is a poimt on the circle such that PC is a tangent to the circle. If PC = 18 cm, and BP = 15 cm, then AB is equal to:
A8.5 cmB6.2 cmC5.8 cmD6.6 cmIn the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
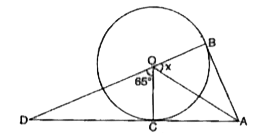 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘
In the given figure A,B is a chord of the circle and AOC is its diameter ,such that ∠ACB=50∘ .If AT is the tangent to the circle at the point A, then ∠BAT is equal to :

View SolutionChord AB of a circle is produced to a point P, and C is a point on the circle such that PC is a tangent to the circle. If PC = 18 cm, and BP = 15 cm, then AB is equal to:
View SolutionIn the figure, BC is a chord of the circle with centre o and A is a point on the minor are BC. Then ∠ABC−∠OBCis equal to
View SolutionEqual chords of a circle are equidistant from circle.
View SolutionIn the adjoining figure, seg AB and seg AD are chords of the circle . C is a point on tangent to the circle at point A. IF m(arc APB)=80∘and ∠BAD=30∘, then find
(i) ∠BAC (ii) m(arc BQD)
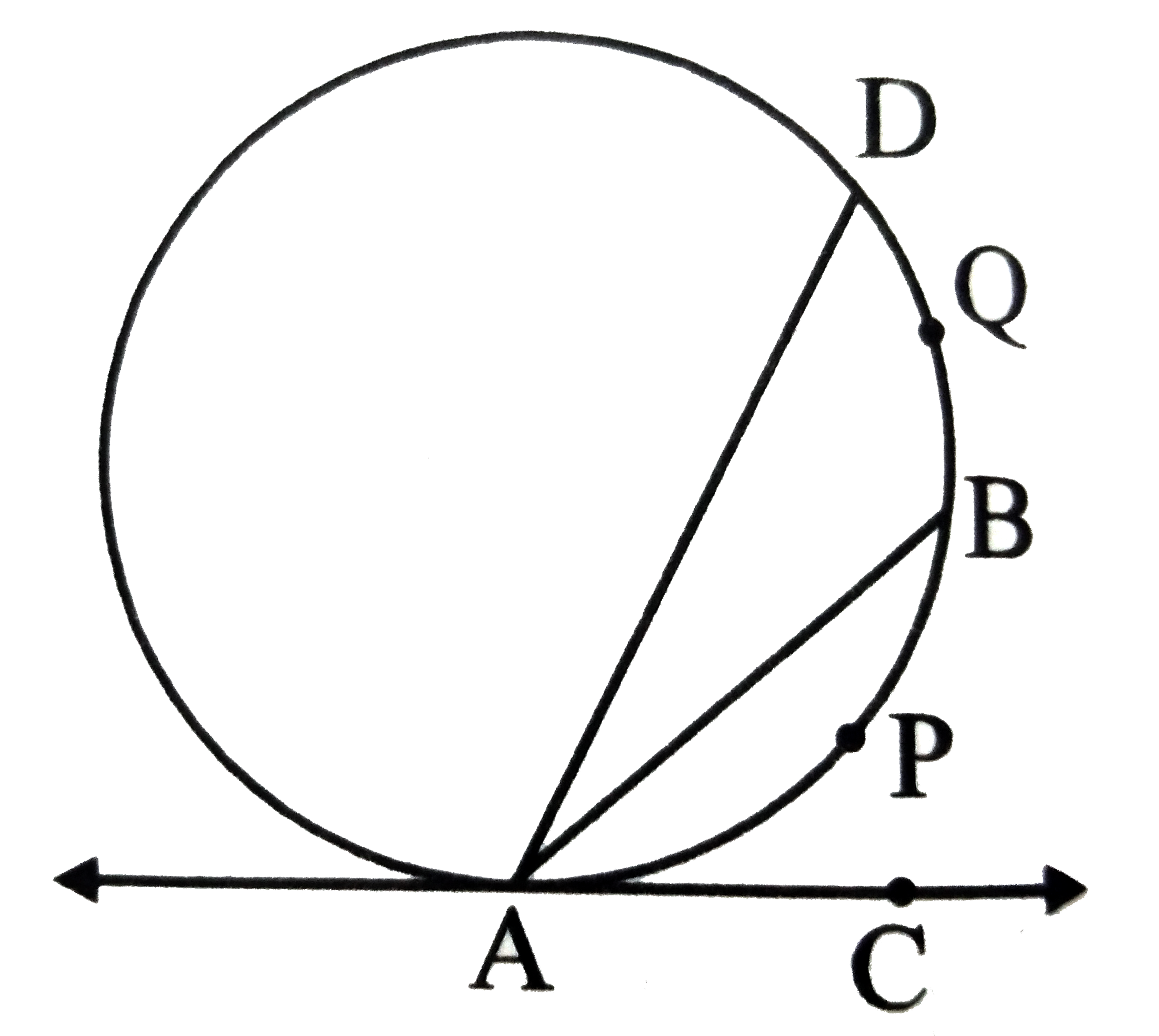
View Solution
