Match the statements/expressions in Column I with the statements/expression in Column II. Column I Column II Root(s) of the equation 2sin2θ+sin22θ=2 (p) π6 Points of discontinuity of the function f(x)=[6xπ]cos[3xπ], where [y] denotes the largest integer less than or equal to y (q) π3 Volume of the parallelepiped with its edges represented by the vectors →a,→band→c are unit vectors satisfying →a+→b+√3→c=→0 (r) π2Solution in Bengali
Step by step video & image solution for Match the statements/expressions in Column I with the statements/expression in Column II. Column I Column II Root(s) of the equation 2sin^2theta+sin^2 2theta=2 (p) pi/6 Points of discontinuity of the function f(x)=[(6x)/pi]cos[(3x)/pi], where [y] denotes the largest integer less than or equal to y (q) pi/3 Volume of the parallelepiped with its edges represented by the vectors vec a , vec ba n d vec c are unit vectors satisfying vec a+ vec b+sqrt(3) vec c= vec0 (r) pi/2 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
The pair of lines joining the origin to the points of intersection of the curves
ax2+2hxy+by2+2gx=0 and
a'x2+2h'xy+b'y2+2g'x=0
will be at right angles to one another , if02:52View SolutionNumber of points of discontinuity of the function f(x)=[(6x)/(pi)]cos[(3x)/(pi)] where [y] denotes the greatest integer function less than or equal to y) in the interval [0,(pi)/(2)] is
05:03View SolutionMatch the conditions/expressions in Column I with statement in Column Ⅱ. (A). sin(π[x]) (B) sin{π(x−[x])}
01:24View SolutionIf →a and →b be two unit vectors and θ is the angle between them. Then →a+→b is an unit vector, if θ= π2 b. 2π3 c. π4 d. π3
02:05View SolutionGivem below in column I are the relations between vectors vec a, vec b and vec c and in column II are that orientations of vec a, vec b and vec C in the (XY) plane . Match therelation in column I to correct orientatlons in column II. Column I , Column II (a) vec a+vec b=vec c , (i) . (b) vec a- vec c =vec b , (ii) . (c ) vec b - vec a =vec c , (iii) . (d) vec a+ vec b+ vec c =0 (iv) .
04:45View SolutionMatch the conditions/ expressions in Column I with statements in Column II.
Let the functions defined in Column I have domain (−π/2,π/2).
(##41Y_SP_MATH_C10_E02_025_Q01.png" width="80%">06:57View SolutionThe points of discontinuities of f(x)=[6xπ]cos[3xπ]in[π6,π] is/are:(where [.] denotes greattest integer function)
03:57View SolutionLet f(x)=x2−6x+5x2−5x+6 Match the expressions/ statements in Column I with expressions / Statement in column II.
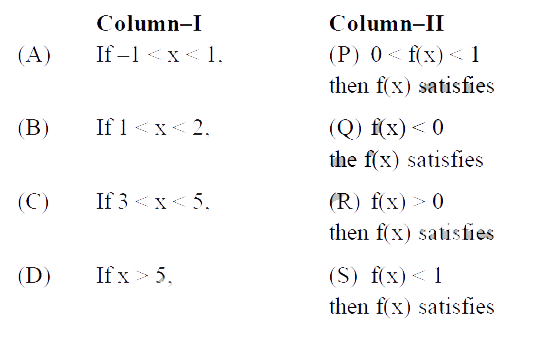 View Solution
View Solutionस्तम्भ I के कथन /व्यंजक को स्तम्भ II के कथन/व्यंजक से सुमेल कीजिए।
 03:36View Solution
03:36View SolutionMatch the statements/expressions in Column I with the statements/expression in Column II. Column I Column II Root(s) of the equation 2sin2θ+sin22θ=2 (p) π6 Points of discontinuity of the function f(x)=[6xπ]cos[3xπ], where [y] denotes the largest integer less than or equal to y (q) π3 Volume of the parallelepiped with its edges represented by the vectors →a,→band→c are unit vectors satisfying →a+→b+√3→c=→0 (r) π2
02:34View SolutionColumn I, Column II Collinear vectors, p.→a Coinitial vectors, q. →b Equal vectors, r. →c Unlike vectors (same intitial point), s. →d
07:36View SolutionVolume of parallelepiped formed by vectors →a×→b,→b×→cand→c×→ais36sq. units. Column I|Column II Volume of parallelepiped formed by vectors →a,→b,and→c is|p. 0sq.units Volume of tetrahedron formed by vectors →a,→b,and→c is|q. 12 sq. units Volume of parallelepiped formed by vectors →a+→b,→b+→cand→c+→a is|r. 6 sq. units Volume of parallelepiped formed by vectors →a−→b,→b−→cand→c−→a is|s. 1 sq. units
02:21View SolutionLet the province of the functions defined in column I (-pi//2,pi//2) And range (-oo,oo) is . Then match the conditions / expressions given in column I with the statements given in column II.
07:46View SolutionColumn - I Column - II A) The number of pairs (x, y) satisfying the equation sin x + sin y = sin (x + y) and |x| + |y| = 1 P) 6 B) The number of values of x satisfying e1√2(esinx+ecosx)=2in(−π,π)isQ) 4 C) The number of values ofx∈(−π,π)satisfying cos7x+sin4x=1isR) 3 D) The number of values of x∈(−π,π)satisfying cos50x−sin50x=1S) 2
07:17View SolutionLet (x,y) be such that sin−1(ax)+cos−1(y)+cos−1(bxy)=π/2. Match the statements in column I which statements in column II.
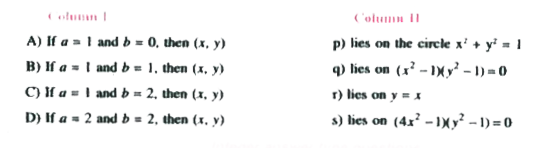 View Solution
View SolutionMatch the statements/ expressions in Column I with the statements/ expressions in Column II.
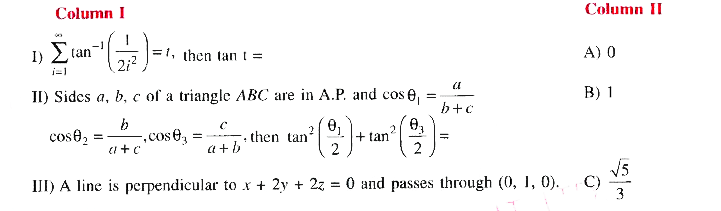 View Solution
View Solution

