The number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π] is (a) 2 (b) 3 (c) 4 (d) 0Solution in Bengali
We have x sin x = 1
∴ sinx=1x
Number of roots of the above equation = number of points (s) of the intersection of the graphs of y=sinx and y=1x for x∈[−2π,0)∪(0,2π]
The graphs of both functions are as shown in the following figure.
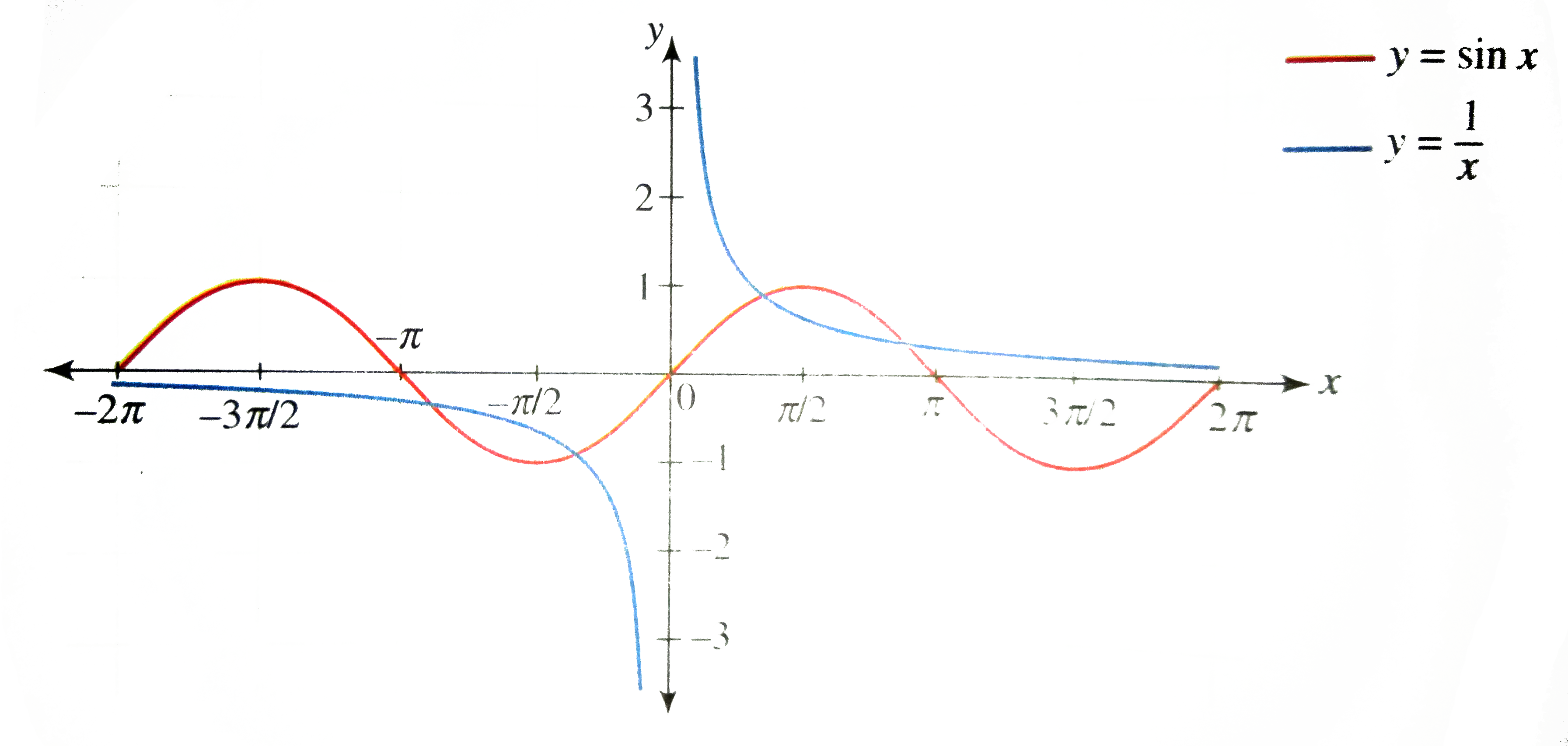
Graphs intersect at four points, hence four roots.
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 6
View SolutionThe number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π] is 2 (b) 3 (c) 4 (d) 0
View SolutionThe number of real roots of equation x8−x5+x2−x+1=0 is (A) 2 (B) 4 (C) 6 (D) 0
View SolutionThe number of real roots (s) of the equation x2tanx=1 lying between 0 and 2π is /are (A) 1 (B) 2 (C) 3 (D) 4
View SolutionLet f(x)=max{tanx,cotx}. Then number of roots of the equation f(x)=1√3∈(0,2π) is (A) 2 (B) 4 (C) 0 (D) infinite
View SolutionFind the number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π].
View SolutionThe number of solutions of the equation tanx+secx=2cosx lying in the interval [0,2π] is 0 (b) 1 (c) 2 (d) 3
View SolutionIf the roots of the equation x2+ax+b=0arecandd, then roots of the equation x2+(2c+a)x+c2+ac+b=0 are a c b. d−c c. 2c d. 0
View SolutionThe number of values of a for which equations x3+ax+1=0andx4+ax2+1=0 have a common root is a) 0 b) 1 c) 2 d) Infinite
View SolutionFind the number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π].
View SolutionIf |cotx+cosecx|=|cotx|+|cosecx|,x∈[0,2π], then complete set of values of x is : (a).[0,π] (b).(0,π2] (c).(0,π2]∪[3π2,2π) (d).(π,3π2]∪[7π4,2π]
View SolutionThe number of real roots of the equation |x|^(2) - 3|x| + 2 = 0 is a)1 b)2 c)3 d)4
View SolutionNumber of roots of equation 3|x|−|2−|x∣∣=1 is a. 0 b. 2 c. 4 d. 7
View SolutionThe number of solution of equation 2cos−1x=a+a2(cos−1x)−1 are at least (a) 1 if a∈[−2π,π]−{0} (b) 1 if a ∈(0,π] (c) 1 if a∈[−2π,0) (d) 2 if a>0
View SolutionNumber of roots of equation 3|x|−|2−|x∣∣=1 is a. 0 b. 2 c. 4 d. 7
View Solution
