There is a point (p,q) on the graph of f(x)=x2 and a point (r,s) on the graph of g(x)=−8x,whereg>0andr>0. If the line through (p,q) and (r,s) is also tangent to both the curves at these points, respectively, then the value of (p+r)is____ Solution in Bengali
Step by step video & image solution for There is a point (p,q) on the graph of f(x)=x^(2) and a point (r,s) on the graph of g(x)=(-8)/(x),"where" g gt0 and rgt0. If the line through (p,q) and (r,s) is also tangent to both the curves at these points, respectively, then the value of (p+r) is "____" by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Given two points A and B. If area of triangle ABC is constant then locus of point C in space is
View SolutionFind the area of the figure enclosed by the curve 5x2+6xy+2y2+7x+6y+6=0.
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
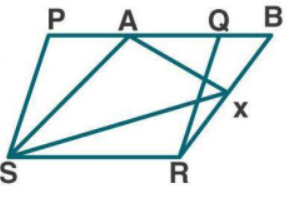
View SolutionThere is a point (p,q) on the graph of f(x)=x2 and a point (r,s) on the graph of g(x)=−8x,wherep>0andr>0. If the line through (p,q)and(r,s) is also tangent to both the curves at these points, respectively, then the value of P+r is_________.
View SolutionIf p,q,r>0 and p!=q!=r such that,f(x)=px^(2)+2qx+r,g(x)=qx^(2)+2rx+p,f(x)=0 and g(x)=0 has a common root.
View SolutionThe tangent at an arbitrary point R on the curve (x^(2))/(p^(2))-(y^(2))/(q^(2))=1 meets the line y=(q)/(p)x at the point S, then the locus of mid-point of RS is
View SolutionThe lines (p-q)x+(q-r)y+(r-p)=0(q-r)x+(r-p)y+(p-q)=0,(x-p)x+(p-q)y+(q-r)=
View SolutionLet f(x)={a2+a+1}+bcosec−1x where aεI and b>0. If range of f(x) is[p,r]∪(r,q], then the value of p2q2+r2 equals
View Solutionp(x)=g(x).q(x)+r(x) లో g(x) , p(x) కు కారణాంకం అయితే r(x) =
View SolutionBy division algorithm for polynomials
P(x)=|g(x)q(x)|+r(x)
P(X)−r(x)=g(x)q(x)
P(x)+{−r(x)}=g(x)q(x)
View SolutionIf p,q,r,s are rational numbers and the roots of f(x)=0 are eccentricities of a parabola and a rectangular hyperbola, where f(x)=px3+qx2+rx+s ,then p+q+r+s= a. p b. −p c. 2p d. 0
View SolutionThere is a point (p,q) on the graph of f(x)=x2 and a point (r,s) on the graph of g(x)=−8x,wherep>0andr>0. If the line through (p,q)and(r,s) is also tangent to both the curves at these points, respectively, then the value of P+r is_________.
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(∣∣gmPQRS)=ar(∣∣gmABRS), ar(△AXS)=12ar(∣∣gmPQRS)
View Solutionफलन f(x)=x2 के आरेख पर एक बिंदु (p,q) है तथा फलन g(x)=−8x के आरेख पर एक बिंदु (r,s) है, जहाँ p>0 तथा r>0 है। यदि ( p,q) तथा ( r,s) से गुजरने वाली रेखा क्रमशः इन बिंदुओं पर दोनों वक्रों पर स्पर्श रेखा है, तो ( p + r ) का मान ज्ञात कीजिये।
View SolutionThe line y = x is a tangent to the curve y=px2+qx+r at the point x =1. If the curve passes through the point (-1, 0) then the value of (p+r)/q is
View SolutionIf p,q,r,s are rational numbers and the roots of f(x)=0 are eccentricities of a parabola and a rectangular hyperbola, where f(x)=px3+qx2+rx+s ,then p+q+r+s= a. p b. −p c. 2p d. 0
View Solution
