Statement 1 : The area bounded by 2≥max { |x-y|,|x+y| } is 8 sq. units. Statement 2 : The area of the square of side length 4 is 16 sq. units.Solution in Bengali
Step by step video & image solution for Statement 1 : The area bounded by 2geq m a x { |x-y|,|x+y| } is 8 sq. units. Statement 2 : The area of the square of side length 4 is 16 sq. units. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
What is the angle between these two curves x3−3xy2+2=0 and 3x2y−y3−2=0
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionStatement 1 : The area bounded by 2≥max.|x−y|,|x|y| is 8 sq. units. Statement 2 : The area of the square of side length 4 is 16 sq. units.
View SolutionThe area of the region bounded by the curves y=|x−1| and y=3−|x| is (A) 6 sq. units (B) 2 sq. units (C) 3 sq. units (D) 4 sq. units
View SolutionThe area (in sq. units) bounded by y=2−|x−2| and the x-axis is
View SolutionThe area (in sq. units) bounded by y=4x−x2 and y=xis
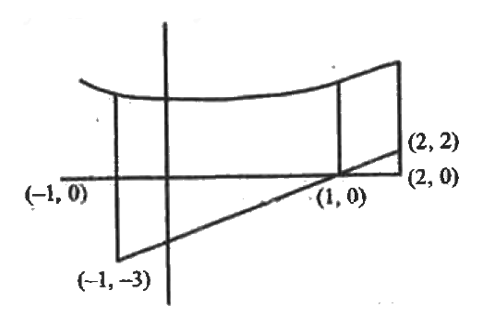
View SolutionThe area (in sq. units) of the region bounded by x=−1,x=2,y=x2+1andy=2x−2 is
View SolutionArea bounded by y=x2 and line y=x is 14 sq unit.
View SolutionThe area bounded by the curves y=|x|−1 and y=−|x|+1 is
View SolutionThe area bounded by the curves y=logex and y=(logex)2 is (A) e−2 sq. units (B) 3−e sq. units (C) e sq. units (D) e−1 sq. units
View SolutionStatement 1 : The area bounded by 2≥max.|x−y|,|x|y| is 8 sq. units. Statement 2 : The area of the square of side length 4 is 16 sq. units.
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 sq. units (b) 2 sq. units 2√2 sq. units (d) 4 sq. units
View SolutionThe area bounded by the parabolas y=(x+1)2 and y=(x−1)2andy=(x−1)2 and the line y=14 is 4 sq. units (b) 1/6 sq. units 4/3 sq. units (d) 1/3 sq. units
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is 1 sq. units (b) 2 sq. units 2√2 sq. units (d) 4 sq. units
View SolutionThe area (in sq. units) bounded by y=2−|x−2| and the x-axis is
View SolutionThe area (in sq. units) bounded by y=4x−x2 and y=xis
View Solution
