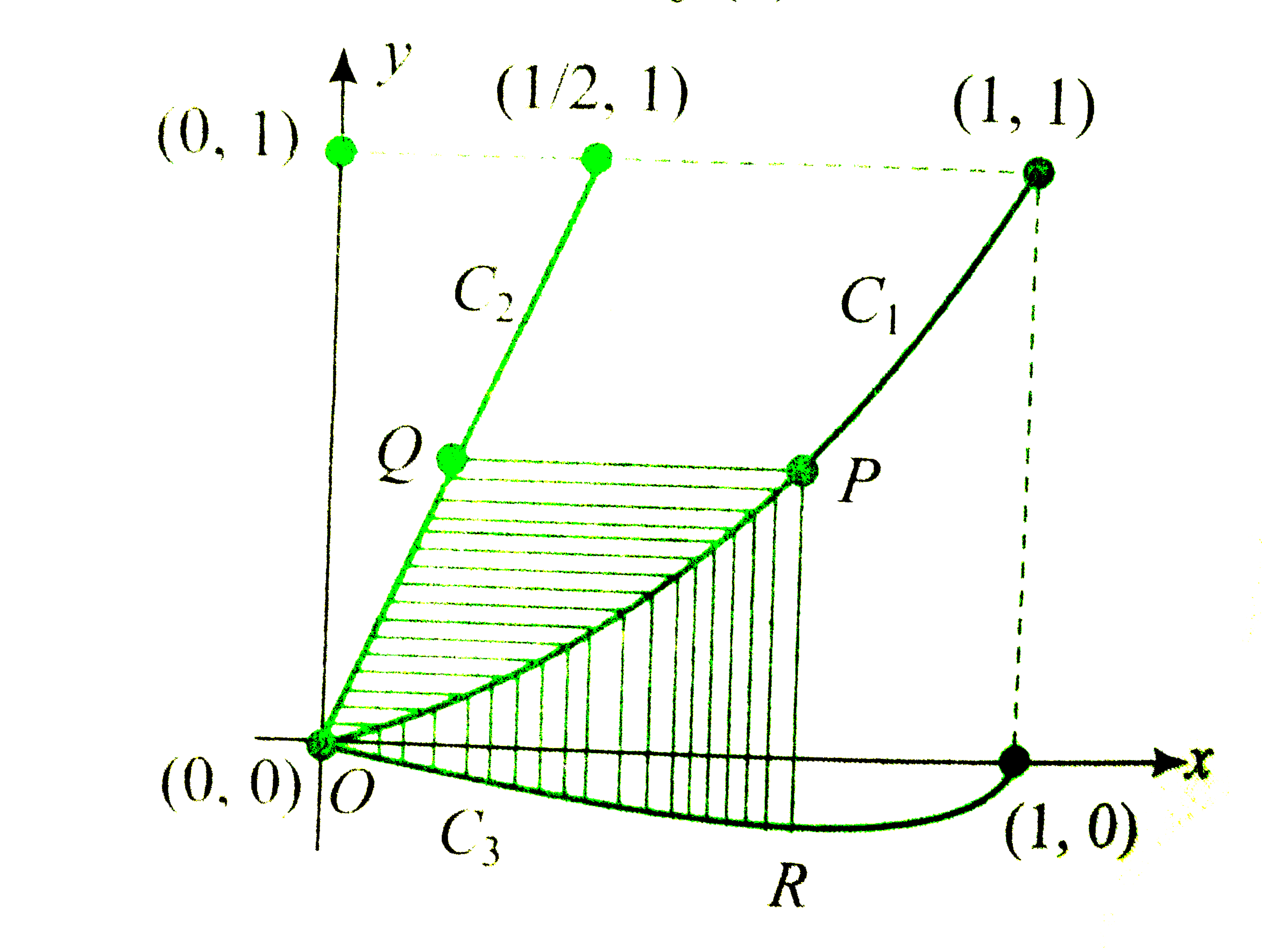
Let C1C2 be the graphs of the functions y=x2 and y=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axis, meet C2 and C3 at Q and R, respectively (see Figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x)Solution in Bengali
Step by step video & image solution for Let C_1C_2 be the graphs of the functions y=x^2 and y=2x , respectively, where 0lt=xlt=1. Let C_3 be the graph of a function y=f(x), where 0lt=xlt=1, f(0) =0. For a point P on C_1, let the lines through P , parallel to the axis, meet C_2 and C_3 at Q and R , respectively (see Figure). If for every position of P(onC_1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
What is the angle between these two curves x3−3xy2+2=0 and 3x2y−y3−2=0
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionLet f(x)=M a xi mu m{x2,(1−x)2,2x(1−x)}, where 0≤x≤1. Determine the area of the region bounded by the curves y=f(x),x-axis ,x=0,andx=1.
View SolutionLet C_1 and C_2, be the graph of the functions y= x^2 and y= 2x, 0<=x<= 1 respectively. Let C_3, be the graph of a function y- (fx), 0<=x<=1, f(0)=0. For a point Pand C_2, let the lines through P, parallel to the axes, meet C_2 and C_3, at Q and R respectively. If for every position of P (on C_1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View SolutionThe points of discontinuity of the function f(x)={2√x , 0≤x≤1, 4−2x , 1<x
View SolutionLet C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View SolutionLet f be a function such that f(x+f(y))=f(f(x))+f(y) ∀x,y∈R and f(h)=h for 0ε
where ε>0, then determine f'(x) and f(x).
View Solutionमाना C1 और C2 क्रमशः फलन y=x2 औरy=2x,0≤x≤1 के ग्राफ हैं। माना C3 फलन, y=f(x),0≤x≤1,f(0)=0 का ग्राफ है। C1 के एक बिंदु P के लिए माना कि बिन्दु P से होकर जाने वाली तथा अक्षों के समान्तर रेखायें C2 व C3 को क्रमशः Q और R पर मिलती है।
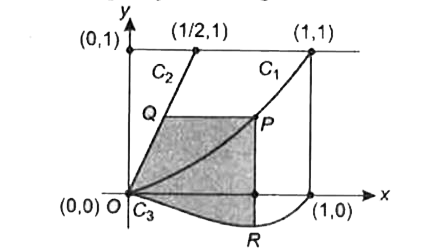 यदिP की प्रत्येक स्थिति ( C1 पर ) के लिए छायांकित क्षेत्र OPQ और ORP का क्षेत्रफल समान हो,तो फलन f(x) को ज्ञात कीजिए।
यदिP की प्रत्येक स्थिति ( C1 पर ) के लिए छायांकित क्षेत्र OPQ और ORP का क्षेत्रफल समान हो,तो फलन f(x) को ज्ञात कीजिए।
View SolutionLet f:[0,1]→[0,1] be a continuous function. Then prove that f(x)=x for at least one 0≤x≤1.
View SolutionIn the hexaploid wheat, the haploid (n) and basic (x) numbers of chromosomes are
View SolutionLet C1C2 be the graphs of the functions y=x2 and y=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axis, meet C2 and C3 at Q and R, respectively (see Figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x)
View SolutionLet C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).

View SolutionThe points of discontinuity of the function f(x)={2√x , 0≤x≤1, 4−2x , 1<x
View SolutionLet f:[0,1]→[0,1] be a continuous function. Then prove that f(x)=x for at least one 0≤x≤1.
View SolutionLet f(x) =M a xi mu m {x^2,(1-x)^2,2x(1-x)}, where 0lt=xlt=1. Determine the area of the region bounded by the curves y=f(x) ,x-axis ,x=0, and x=1.
View SolutionLet C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).

View Solution
